题目内容
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上不与点
上不与点![]() 重合的一个动点.
重合的一个动点.
(1)求线段![]() 的长;
的长;
(2)当![]() 的面积是6时,求点
的面积是6时,求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,若存在,请直接写出所有符合条件的点
全等,若存在,请直接写出所有符合条件的点![]() 的坐标,否则,说明理由.
的坐标,否则,说明理由.

【答案】(1)![]() ; (2) (-4,6); (3) (
; (2) (-4,6); (3) (![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)先求得点A、B的坐标,可求得OA、OB、AB的长,利用面积法即可求得OM的长;
(2)先画图,确定△BOP面积可以BO为底,P到y轴距离为高求得P到y轴距离,再分类讨论求得答案;
(3)分△OMP≌△PQO与△OMP≌△OQP两种情况讨论,结合图象分析即可求解.
(1)对于直线![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
点A、B的坐标分别是(4,0),(0,3),
∴OA=4,OB=3,AB=![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)过P作PC⊥y轴于C,如图1,
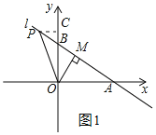
∴![]() OBPC=6,
OBPC=6,
∴PC=4,
∴点P的横坐标为4或-4,
∵点P为直线![]() 上的一个动点且不与A、B重合,
上的一个动点且不与A、B重合,
∴横坐标为4时,与A重合,不合题意,
∴横坐标为-4时,纵坐标为:![]()
∴当点P坐标为(-4,6)时,△BOP的面积是6;
(3)存在,理由如下:
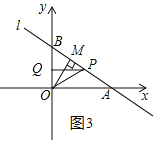
①当△OMP≌△PQO时,如图2和图3,
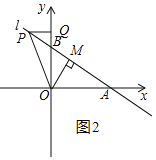
由(1)得![]() ,
,
∴PQ=OM=![]() ,即P点横坐标为
,即P点横坐标为![]() 或
或![]() ,
,
纵坐标为:![]() 或
或![]() ,
,
此时点P的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() );
);
②当△OMP≌△OQP时,如图4和图5,
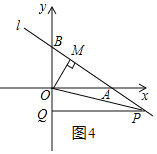
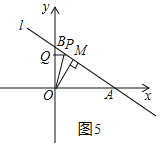
∴OQ=OM=![]() ,即即点P、点Q纵坐标为
,即即点P、点Q纵坐标为![]() 或
或![]() ,
,
由![]() ,解得:
,解得:![]() ;
;
由![]() ,解得:
,解得:![]() ;
;
此时点P的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() );
);
综上所述,符合条件的点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) .
) .

【题目】某中学八年级组织了一次“汉字听写比赛”,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,语文教研组将八年级一班和二班的成绩整理并绘制成如下的统计图,请根损换供的信息解答下列问题.
(1)把一班比赛成统计图补充完整;

(2)填表:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 85 |
二班 | 84 | 75 | c |
表格中:a=______,b=______,c=_______.
(3)请从以下给出的两个方面对这次比赛成绩的结果进行分析:
①从平均数、众数方面来比较一班和二班的成绩;
②从B级以上(包括B级)的人数方面来比较-班和二班的成绩.