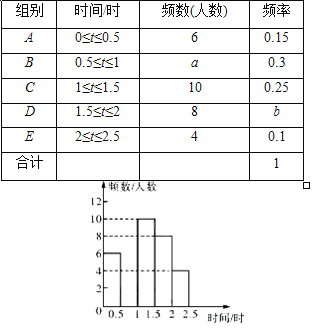
0 325410 325418 325424 325428 325434 325436 325440 325446 325448 325454 325460 325464 325466 325470 325476 325478 325484 325488 325490 325494 325496 325500 325502 325504 325505 325506 325508 325509 325510 325512 325514 325518 325520 325524 325526 325530 325536 325538 325544 325548 325550 325554 325560 325566 325568 325574 325578 325580 325586 325590 325596 325604 366461
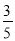 ,则对角线AC的长为____.
,则对角线AC的长为____. 
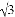 -
-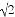 |+(
|+(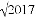 -1)0+2sin45°-2cos30°+(
-1)0+2sin45°-2cos30°+(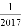 )-1
)-1 ,其中a=
,其中a=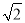 -1.
-1.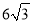 米,斜坡BC的坡度i=1:
米,斜坡BC的坡度i=1: 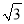 .小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.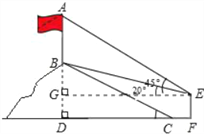
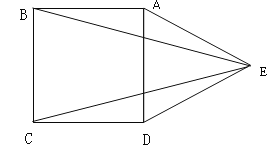
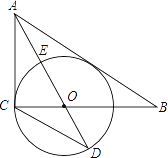
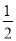 ,求
,求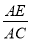 的值.
的值. 
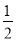 ,求
,求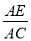 的值.
的值. 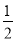 (3)
(3)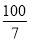
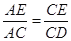 = tanD=
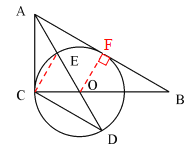
= tanD=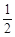 ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得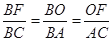 ,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
,设BO="y" ,BF=z,列二元一次方程组即可解决问题.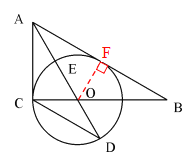
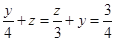
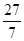 y=
y=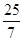
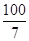
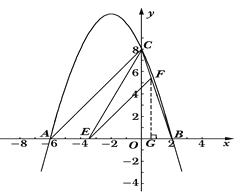
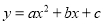 的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).