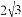0 325409 325417 325423 325427 325433 325435 325439 325445 325447 325453 325459 325463 325465 325469 325475 325477 325483 325487 325489 325493 325495 325499 325501 325503 325504 325505 325507 325508 325509 325511 325513 325517 325519 325523 325525 325529 325535 325537 325543 325547 325549 325553 325559 325565 325567 325573 325577 325579 325585 325589 325595 325603 366461
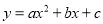 的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).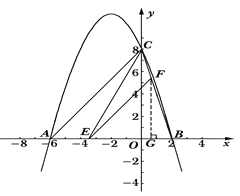
 x2-
x2- x+8(2)
x+8(2) x2-
x2- x+8
x+8 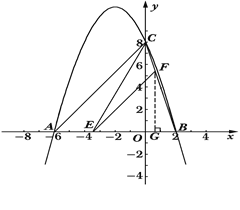
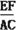 =
=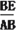 . 即
. 即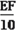 =
=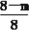 . ∴EF=
. ∴EF=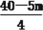 .
. .∴
.∴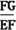 =
=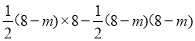
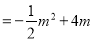 (0<m<8)
(0<m<8)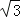 ,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题:
,直角边CD在y轴上,且点C与点A重合.Rt△CDE沿y轴正方向平行移动,当点C运动到点O时停止运动.解答下列问题: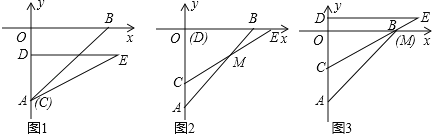
 D.
D. 
 B. m≤
B. m≤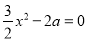 的一个解,则2a-1的值是( )
的一个解,则2a-1的值是( )