如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段AB',则点B'的坐标为_____.
(4,2)
【解析】试题分析：画出旋转后的图形位置，根据图形求解．
试题解析：AB旋转后位置如图所示．
B′（4，2）． 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．
。
【解析】试题分析：根据矩形的性质得∠B=∠D=∠BAD=90°，根据旋转的性质得∠D′=∠D=90°，∠4=α，利用对顶角相等得到∠1=∠2=110°，再根据四边形的内角和为360°可计算出∠3=70°，然后利用互余即可得到∠α的度数．
【解析】
如图，
∵四边形ABCD为矩形，
∴∠B=∠D=∠BAD=90°，
∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′... 在边长为1个单位长度的小正方形组成的网格中，点A、B、C、O都是格点．
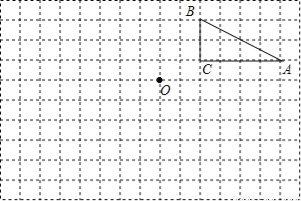
（1）将△ABC向左平移6个单位得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕点O按逆时针方向旋转180°得到△A2B2C2，请画出△A2B2C2．
（1）作图见解析；（2）作图见解析.
【解析】试题分析：（1）把A、B、C三点分别向左平移6个单位长度，即可得到三个顶点的对应点，然后顺次连接三点即可；
（2）连接AO并延长，然后截取OA2=OA，则A2就是A的对应点，同样可以作出B、C的对应点，然后顺次连接即可．
【解析】
（1）所作图形如图所示；
（2）所作图形如图所示． 如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.
（1）操作发现
如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：
①线段DE与AC的位置关系是_________；
②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是____________.
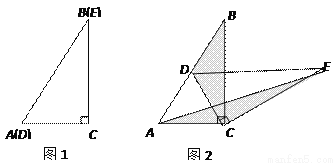
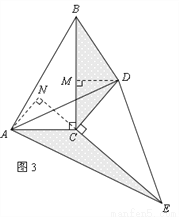
（2）猜想论证
当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想.
（3）拓展探究
已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE//AB交BC于点E（如图4）.若在射线BA上存在点F，使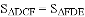
，请直接写出相应的BF的长.
（1）①DE∥AC；②S1＝S2；（2）证明见解析；（3）BF的长为或.
【解析】试题分析：（1）①根据旋转的性质可得AC=CD，然后求出△ACD是等边三角形，根据等边三角形的性质可得∠ACD=60°，然后根据内错角相等，两直线平行解答；
②根据等边三角形的性质可得AC=AD，再根据直角三角形30°角所对的直角边等于斜边的一半求出AC=AB，然后求出AC=BD，再根据等边三角形的性质求... 对数轴上的点P进行如下操作：先把点P表示的数乘以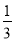
，再把所得数对应的点向右平移1个单位，得到点P的对应点P′，点A，B在数轴上，对线段AB上的每个点进行上述操作后得到线段A′B′，其中点A，B的对应点分别为A′，B′，如图，若点A表示的数是﹣3，则点A′表示的数是__；若点B′表示的数是2，则点B表示的数是__．已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合，则点E表示的数是__．
0 3 1.5
【解析】试题分析：根据题目规定，以及数轴上的数向右平移用加计算即可求出点A′，设点B表示的数为a，根据题意列出方程求解即可得到点B表示的数，设点E表示的数为b，根据题意列出方程计算即可得解．
试题解析：【解析】
点A′：﹣3×+1=﹣1+1=0．
设点B表示的数为a，则a+1=2，解得a=3．
设点E表示的数为b，则b+1=b，解得b=1.5．
故答... 如图，从地面竖直向上抛出一个小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的关系式为h=30t-5t2，那么小球从抛出至回落到地面所需要的时间是（ ）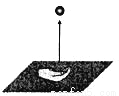
A. 6s B. 4s C. 3s D. 2s
A
【解析】试题分析：由小球高度h与运动时间t的关系式h=30t﹣5t2，令h=0，解得的两值之差便是所要求得的结果．
由小球高度h与运动时间t的关系式h=30t﹣5t2． 令h=0，﹣5t2+30t=0 解得：t1=0，t2=6
△t=6，小球从抛出至回落到地面所需要的时间是6秒． 如图，在平面直角坐标系中，四边形OBCD是边长为4的正方形，平行于对角线BD的直线l从O出发，沿x轴正方向以每秒1个单位长度的速度运动，运动到直线l与正方形没有交点为止．设直线l扫过正方形OBCD的面积为S，直线l运动的时间为t(秒)，下列能反映S与t之间函数关系的图象是( )
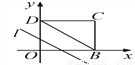
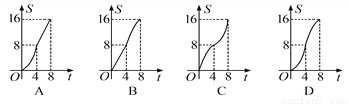
A. A B. B C. C D. D
D
【解析】试题分析：根据三角形的面积即可求出S与t的函数关系式，根据函数关系式选择图象．
试题解析：如图：
①当0≤t≤4时，S=×t×t=t2，即S=t2．
该函数图象是开口向上的抛物线的一部分．
故B、C错误；
②当4＜t≤8时，S=16-×（8-t）×（8-t）=-t2+8t-16．
该函数图象是开口向下的抛物线的一部分．
故A错误．
... 在羽毛球比赛中，某次羽毛球的运动路线可以看做是抛物线y＝－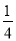
x2＋bx＋c的一部分(如图)，其中出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，那么这条抛物线的表达式是( )
A. y＝－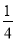
x2＋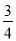
x＋1 B. y＝－
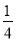x2＋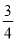
x－1 C. y＝－
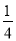x2－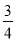
x＋1 D. y＝－
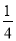x2－
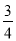x－1
A
【解析】根据已知出球点B离地面O点的距离是1m，球落地点A到O点的距离是4m，得出B点的坐标为：（0，1），A点坐标为（4，0），代入解析式y＝－x2＋bx＋c，即可求出b=，c=1，即可得出这条抛物线的解析式是：y=-x2+x+1．
故选：A． 如图，有一抛物线拱桥，当水位线在AB位置时，拱桥顶离水面2m，水面宽4m，水面下降1m后，水面宽为( )
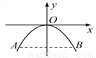
A. 5m B. 6m C.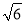 
m D. 2
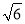m
D
【解析】试题分析：建立如图所示的坐标系，则点A的坐标为（-2，-2），设函数关系式为，则-2=4a，所以a= -，所以，当y=-3时， ，所以水面宽为m，故选：D． 如图为某菜农搭建的一个横截面为抛物线的大棚，有关尺寸如图所示，某菜农身高1.6米，则他在不弯腰的情况下在大棚内左右活动的范围是( )
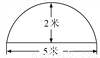
A.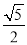 
米 B.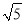 
米 C. 1.6米 D. 0.8米
B
【解析】如图，设抛物线的解析式为y=a（x-2.5）2+2，由待定系数法求出抛物线的解析式y=- （x-2.5）2+2，将y=1.6时代入解析式得- （x-2.5）2+2=1.6，解得， ，他在不弯腰的情况下在大棚里活动的范围是：x1-x2=．
故选：B.