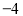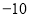声音在空气中传播的速度y(m/s)(简称声速)与气温x(℃)的关系如下表所示.
气温x/℃ | 0 | 5 | 10 | 15 | 20 |
声速y/(m/s) | 331 | 334 | 337 | 340 | 343 |
上表中___________是自变量, __________是因变量.照此规律可以发现,当气温x为__________℃时,声速y达到346 m/s.
气温 声速 25 【解析】气温是自变量, 声速是因变量 设函数解析式y=kx+b, ∵该函数图象经过点(0,331)和(5,334), ∴, 解得. ∴该函数关系式为y=x+331 . 当y=346时,x=25 即当气温x为25 ℃时,声速y达到346 m/s. 故答案为:25 故答案为:气温 声速 25弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:
x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
下列说法不正确的是( )
A. x与y都是变量,且x是自变量,y是因变量
B. 弹簧不挂重物时的长度为0 cm
C. 物体质量每增加1 kg,弹簧长度y增加0.5 cm
D. 所挂物体质量为7 kg时,弹簧长度为13.5 cm
B 【解析】A. x与y都是变量,且x是自变量,y是因变量,故A正确;物 B. 体的质量为零时,弹簧的长度为10厘米,故B错误;; C. 物体质量每增加1kg,弹簧长度y增加0.5cm,故C正确; D. 所挂物体质量为7kg时,弹簧长度为13.5cm,故D正确; 故选:B.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t,估计当x=3.2千克时,t的值为( )
A. 140 B. 138 C. 148 D. 160
C 【解析】观察表格可知,烤鸭的质量每增加0.5千克,烤制时间增加20分钟,由此可判断烤制时间是烤鸭质量的一次函数,设烤制时间为t分钟,烤鸭的质量为x千克,t与x的一次函数关系式为:t=kx+b,取(1,60),(2,100)代入,运用待定系数法求出函数关系式,再将x=3.2千克代入即可求出烤制时间t. 【解析】 从表中可以看出,烤鸭的质量每增加0.5千克,烤制的时间增加20分钟,由...赵先生手中有一张记录他从出生到24岁期间的身高情况表(见下表):
年龄x/岁 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
身高h/cm | 48 | 100 | 130 | 140 | 150 | 158 | 165 | 170 | 170.4 |
下列说法错误的是( )
A. 赵先生的身高增长速度总体上先快后慢
B. 赵先生的身高在21岁以后基本不长了
C. 赵先生的身高从0岁到24岁平均每年增高7.1cm
D. 赵先生的身高从0岁到24岁平均每年增高5.1cm
C 【解析】利用统计表给出的数据,逐项分析得出答案即可. 【解析】 A、从0﹣18增长较快,18﹣24增长变慢,所以高增长速度总体上先快后慢是正确的; B、从21岁步入成年,身高在21岁以后基本不长了是正确的; C、(170.4﹣48)÷24=5.1cm,从0岁到24岁平均每年增高7.1cm是错误的; D、(170.4﹣48)÷24=5.1cm,从0岁到24岁平均每...父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了下面的表格。
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 |
|
|
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答。
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你能猜出距离地面6千米的高空温度是多少吗?
(1)上表反映了温度和高度两个变量之间.高度是自变量,温度是因变量. (2)如果用h表示距离地面的高度,用t表示温度,那么随着高度h的增大,温度t逐渐减小(或降低). (3)距离地面6千米的高空温度是-16℃. 【解析】(1)根据图表,反映的是距离地面的高度和温度两个量,所以温度和高度是两个变化的量,温度随高度的变化而变化; (2)根据表格数据,高度越大,时间越低,所以随着...在烧水时,水温达到100 ℃就会沸腾,下表是某同学做“观察水的沸腾”试验时记录的数据:
时间/min | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | … |
温度/℃ | 30 | 44 | 58 | 72 | 86 | 100 | 100 | 100 | … |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间每推移2 min,水的温度如何变化?
(4)时间为8 min时,水的温度为多少?你能得出时间为9 min时水的温度吗?
(5)根据表格,你认为时间为16 min和18 min时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
(1)上表反映了水的温度与时间的关系,时间是自变量,水的温度是因变量. (2)水的温度随着时间的增加而增加,到100 ℃时恒定. (3)时间每推移2 min,水的温度增加14 ℃,到10 min时恒定. (4)时间为8 min时,水的温度是86 ℃,时间为9 min时,水的温度是93 ℃. (5)温度均为100 ℃. (6)应在第10 min后停止烧水. 【解析...心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:min)之间有如下关系(其中0≤x≤20):
提出概念所 用时间x/min | 2 | 5 | 7 | 10 | 12 | 13 | 14 | 17 | 20 |
对概念的接 受能力y | 47.8 | 53.5 | 56.3 | 59 | 59.8 | 59.9 | 59.8 | 58.3 | 55 |
(注:接受能力值越大,说明学生的接受能力越强)
(1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当提出概念所用时间是10 min时,学生的接受能力是多少?
(3)根据表格中的数据,你认为提出概念所用时间为多少时,学生的接受能力最强?
(4)从表格中可知,当提出概念所用时间x在什么范围内时,学生的接受能力逐步增强?当提出概念所用时间x在什么范围内时,学生的接受能力逐步降低?
(1)反映了提出概念所用的时间x和对概念的接受能力y两个变量之间的关系;其中x是自变量,y是因变量. (2) 59. (3)所用时间为13 min时,学生的接受能力最强. (4)当x在2至13的范围内,学生的接受能力逐步增强;当x在13至20的范围内,学生的接受能力逐步降低. 【解析】分析:(1)由条件可知两个变量是提出概念所用的时间和对概念的接受能力,对概念的接受能力随着...