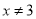0 321080 321088 321094 321098 321104 321106 321110 321116 321118 321124 321130 321134 321136 321140 321146 321148 321154 321158 321160 321164 321166 321170 321172 321174 321175 321176 321178 321179 321180 321182 321184 321188 321190 321194 321196 321200 321206 321208 321214 321218 321220 321224 321230 321236 321238 321244 321248 321250 321256 321260 321266 321274 366461
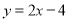 的图像,并完成下列问题:
的图像,并完成下列问题: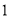 )此函数图像与坐标轴围成的三角形的面积是______;
)此函数图像与坐标轴围成的三角形的面积是______;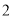 )观察图像,当
)观察图像,当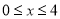 时,y的取值范围是______;
时,y的取值范围是______;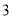 )将直线
)将直线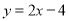 平移后经过点
平移后经过点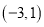 ,求平移后的直线的函数表达式.
,求平移后的直线的函数表达式.
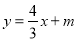 的图像与x轴交于点A
的图像与x轴交于点A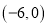 ,交y轴于点B.
,交y轴于点B.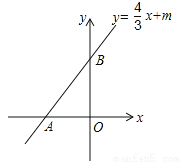
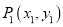 ,
, 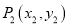 ,我们把
,我们把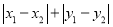 叫做
叫做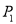 、
、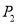 两点间的“转角距离”,记作
两点间的“转角距离”,记作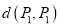 .
.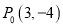 ,O为坐标原点,则
,O为坐标原点,则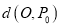 = ;
= ;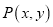 满足
满足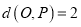 ,请写出x与y之间满足的关系式,并在所给的直角坐标系中,画出所有符合条件的点P所组成的图形;
,请写出x与y之间满足的关系式,并在所给的直角坐标系中,画出所有符合条件的点P所组成的图形;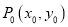 是一个定点,
是一个定点, 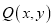 是直线
是直线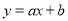 上的动点,我们把
上的动点,我们把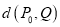 的最小值叫做
的最小值叫做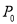 到直线
到直线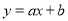 的“转角距离”.若
的“转角距离”.若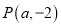 到直线
到直线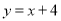 的“转角距离”为10,求a的值.
的“转角距离”为10,求a的值.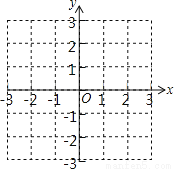
 )请解释图中点C的实际意义;
)请解释图中点C的实际意义; )求出甲、乙在整个过程中的函数表达式(并注明自变量的范围);
)求出甲、乙在整个过程中的函数表达式(并注明自变量的范围); )如果甲、乙两人完成同样数量的零件时,甲比乙少用1小时,那么此时甲、乙两人各自完成多少个零件?
)如果甲、乙两人完成同样数量的零件时,甲比乙少用1小时,那么此时甲、乙两人各自完成多少个零件?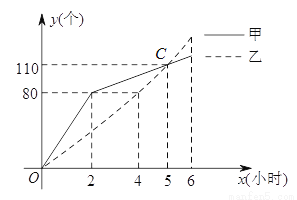

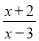 有意义,则
有意义,则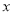 满足的条件是( )
满足的条件是( )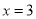 B.
B. 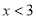 C.
C. 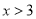 D.
D.