某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
(1)y=﹣0.1x2+0.6x+1; (2)年利润W(万元)与广告费用x(万元)的函数关系式为W=﹣x2+5x+10,每年投入的广告费是2.5万元时所获得的利润最大为16.25万元;(3)1≤x≤4时,年利润W(万元)不低于14万元. 【解析】试题分析:(1)二次函数的解析式为利用表格数据,即可求出与之间的函数关系式; (2)根据利润看作是销售总额减去成本费和广告费,利用配方法,结...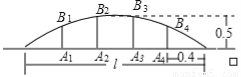
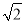 ≈1.41,
≈1.41, 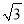 ≈1.73)
≈1.73)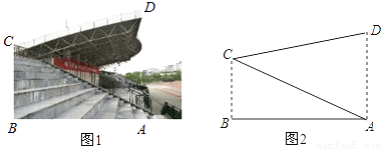
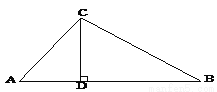
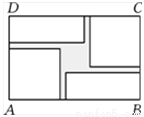
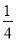 ,若道路与观赏亭的面积之和是矩形水池面积的
,若道路与观赏亭的面积之和是矩形水池面积的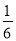 ,求道路的宽.
,求道路的宽.