若一元二次方程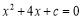
有两个不相等的实数根，则c的值可以是 （写出一个即可）.
抛物线y=2x2﹣3x+4与y轴的交点坐标是______．
查看答案如图是二次函数y=ax2+bx+c过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac，②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确结论是（ ）
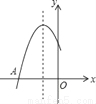
A. ②④ B. ①④ C. ②③ D. ①③
查看答案设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+a上的三点，则y1，y2，y3的大小关系为（ ）
A. y1＞y2＞y3 B. y1＞y3＞y2 C. y3＞y2＞y1 D. y3＞y1＞y2
查看答案在同一坐标系中，一次函数y＝－mx＋n2与二次函数y＝x2＋m的图象可能是（ ）
A. 
B. 
C. 
D. 
关于x的一元二次方程x2﹣3x+m=0没有实数根，则实数m的取值范围为（ ）
A. 
B. 
C. 
D. 
- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知抛物线y＝ax2－3x＋c(a≠0)经过点(－2，4)，则4a＋c－1＝____．
-3 【解析】把(－2，4)代入得： ，∴4a+c=-2，∴4a＋c－1=-2-1=-3．若一元二次方程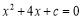有两个不相等的实数根，则c的值可以是 （写出一个即可）.
抛物线y=2x2﹣3x+4与y轴的交点坐标是______．
查看答案如图是二次函数y=ax2+bx+c过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac，②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确结论是（ ）
A. ②④ B. ①④ C. ②③ D. ①③
查看答案设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+a上的三点，则y1，y2，y3的大小关系为（ ）
A. y1＞y2＞y3 B. y1＞y3＞y2 C. y3＞y2＞y1 D. y3＞y1＞y2
查看答案在同一坐标系中，一次函数y＝－mx＋n2与二次函数y＝x2＋m的图象可能是（ ）
A. B. C. D.
- 题型：填空题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是_____%．
20 【解析】设该药品平均每次降价的百分率为x，根据降价后的价格=降价前的价格（1-降价的百分率），则第一次降价后的价格是25（1-x），第二次后的价格是25（1-x）2，据此即可列方程求解． 【解析】 设该药品平均每次降价的百分率为x， 由题意可知经过连续两次降价，现在售价每盒16元， 故25（1-x）2=16， 解得x=0.2或1.8（不合题意，舍去）， 故该药品平均每次...已知抛物线y＝ax2－3x＋c(a≠0)经过点(－2，4)，则4a＋c－1＝____．
查看答案若一元二次方程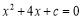有两个不相等的实数根，则c的值可以是 （写出一个即可）.
抛物线y=2x2﹣3x+4与y轴的交点坐标是______．
查看答案如图是二次函数y=ax2+bx+c过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac，②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确结论是（ ）
A. ②④ B. ①④ C. ②③ D. ①③
查看答案设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+a上的三点，则y1，y2，y3的大小关系为（ ）
A. y1＞y2＞y3 B. y1＞y3＞y2 C. y3＞y2＞y1 D. y3＞y1＞y2
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
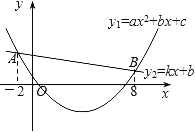
已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+b（k≠0）的图象相交于点A（﹣2，4），B（8，2）（如图所示），则能使y1＞y2成立的x的取值范围是 ．
某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是_____%．
查看答案已知抛物线y＝ax2－3x＋c(a≠0)经过点(－2，4)，则4a＋c－1＝____．
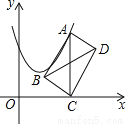
查看答案若一元二次方程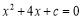有两个不相等的实数根，则c的值可以是 （写出一个即可）.
抛物线y=2x2﹣3x+4与y轴的交点坐标是______．
查看答案如图是二次函数y=ax2+bx+c过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac，②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确结论是（ ）
A. ②④ B. ①④ C. ②③ D. ①③
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
用适当的方法解下列方程．
①（2x+3）2﹣16=0；
②2x2=3（2x+1）．
【解析】 ①∴x1=，x2=﹣；②∴x1=，x2=． 【解析】试题分析：先观察方程，再确定各方程的解法；①用直接开平方法，②根据题意用公式法求解．需注意②先要将方程化为一般式． 试题解析：【解析】 ①（2x+3）2﹣16=0， ∴（2x+3）2=16， ∴2x+3=±4， ∴x1=，x2=﹣； ②2x2=3（2x+1）， 原方程可化为：2x2﹣6x﹣3...如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+b（k≠0）的图象相交于点A（﹣2，4），B（8，2）（如图所示），则能使y1＞y2成立的x的取值范围是 ．
某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是_____%．
查看答案已知抛物线y＝ax2－3x＋c(a≠0)经过点(－2，4)，则4a＋c－1＝____．
查看答案若一元二次方程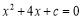有两个不相等的实数根，则c的值可以是 （写出一个即可）.
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知关于x的方程x2＋ax＋a－2＝0.
(1)若该方程的一个根为1，求a的值及该方程的另一个根；
(2)求证：不论a取何实数，该方程都有两个不相等的实数根．
(1)a的值为，该方程的另一个根为－ (2)证明见解析 【解析】（1）试题分析：把1代入方程求出a的值，再把a代入方程，解方程. 试题解析： 把x=1代入方程， 所以a=，再代入方程， ，解得方程的另一个根为﹣. （2）∵△=a2﹣4（a﹣2）=a2﹣4a+8=a2﹣4a+4+4=（a﹣2）2+4＞0， ∴不论a取何实数，该方程都有两个不相等的实数根．用适当的方法解下列方程．
①（2x+3）2﹣16=0；
②2x2=3（2x+1）．
查看答案如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+b（k≠0）的图象相交于点A（﹣2，4），B（8，2）（如图所示），则能使y1＞y2成立的x的取值范围是 ．
某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是_____%．
查看答案已知抛物线y＝ax2－3x＋c(a≠0)经过点(－2，4)，则4a＋c－1＝____．
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．
（1）如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
【解析】 （1）△ABC是等腰三角形，理由见解析； （2）△ABC是直角三角形，理由见解析； （3）x1=0，x2=﹣1． 【解析】试题分析：（1）直接将x=-1代入得出关于a，b的等式，进而得出a=b，即可判断△ABC的形状； （2）利用根的判别式进而得出关于a，b，c的等式，进而判断△ABC的形状； （3）利用△ABC是等边三角形，则a=b=c，进而代入方程求出...已知关于x的方程x2＋ax＋a－2＝0.
(1)若该方程的一个根为1，求a的值及该方程的另一个根；
(2)求证：不论a取何实数，该方程都有两个不相等的实数根．
查看答案用适当的方法解下列方程．
①（2x+3）2﹣16=0；
②2x2=3（2x+1）．
查看答案如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+b（k≠0）的图象相交于点A（﹣2，4），B（8，2）（如图所示），则能使y1＞y2成立的x的取值范围是 ．
某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是_____%．
查看答案 试题属性- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
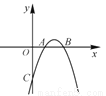
已知抛物线y=ax2+bx+c与x轴交于点A(1，0)，B(3，0)，且过点C(0，-3).
(1)求抛物线的解析式和顶点坐标；
(2)请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=-x上，并写出平移后抛物线的解析式.
已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．
（1）如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
查看答案已知关于x的方程x2＋ax＋a－2＝0.
(1)若该方程的一个根为1，求a的值及该方程的另一个根；
(2)求证：不论a取何实数，该方程都有两个不相等的实数根．
查看答案用适当的方法解下列方程．
①（2x+3）2﹣16=0；
②2x2=3（2x+1）．
查看答案如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+b（k≠0）的图象相交于点A（﹣2，4），B（8，2）（如图所示），则能使y1＞y2成立的x的取值范围是 ．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
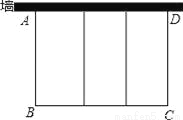
如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？
已知抛物线y=ax2+bx+c与x轴交于点A(1，0)，B(3，0)，且过点C(0，-3).
(1)求抛物线的解析式和顶点坐标；
(2)请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=-x上，并写出平移后抛物线的解析式.
已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．
（1）如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
查看答案已知关于x的方程x2＋ax＋a－2＝0.
(1)若该方程的一个根为1，求a的值及该方程的另一个根；
(2)求证：不论a取何实数，该方程都有两个不相等的实数根．
查看答案用适当的方法解下列方程．
①（2x+3）2﹣16=0；
②2x2=3（2x+1）．
查看答案如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧