直线y=x+3上有一点P(3,a)，则点P关于原点的对称点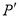
为___________.
如图，两个反比例函数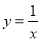
和
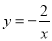的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则△PAB的面积为（ ）
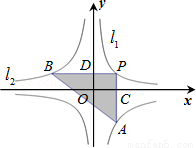
A. 3 B. 4 C.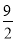 
D. 5
如图是二次函数y=ax2+bx+c的图象，下列结论： ①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为﹣1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
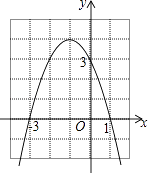
A. 1个 B. 2个 C. 3个 D. 4个
查看答案某同学在用描点法画二次函数y=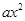
+bx+c的图象时，列出了下面的表格：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣5 | … |
由于粗心，他算错了其中一个y值，则这个错误的数值是（ ）.
A．﹣11 B．﹣2 C．1 D．﹣5
查看答案若圆锥的底面积为16πcm2，母线长为12cm，则它的侧面展开图的圆心角为( )
A. 240° B. 120° C. 180° D. 90°
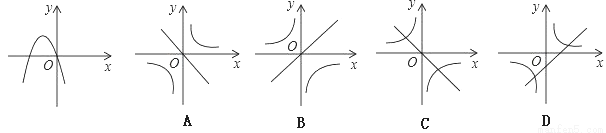
查看答案已知二次函数y=ax2+bx+c的图象如图所示，那么一次函数y=bx+c和反比例函数y=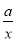
在同一平面直角坐标系中的图象大致是（ ）
- 题型：填空题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
若抛物线y＝x2－2x－3与x轴分别交于A，B两点，则AB的长为 ______．
4 【解析】先求出二次函数与x轴的2个交点坐标，然后再求出2点之间的距离． 【解析】 二次函数y=x2-2x-3与x轴交点A、B的横坐标为一元二次方程x2-2x-3=0的两个根，求得x1=-1，x2=3，则AB=|x2-x1|=4．直线y=x+3上有一点P(3,a)，则点P关于原点的对称点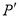为___________.
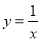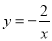如图，两个反比例函数和的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则△PAB的面积为（ ）
A. 3 B. 4 C. 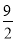D. 5
如图是二次函数y=ax2+bx+c的图象，下列结论： ①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为﹣1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案某同学在用描点法画二次函数y=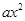+bx+c的图象时，列出了下面的表格：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣5 | … |
由于粗心，他算错了其中一个y值，则这个错误的数值是（ ）.
A．﹣11 B．﹣2 C．1 D．﹣5
查看答案若圆锥的底面积为16πcm2，母线长为12cm，则它的侧面展开图的圆心角为( )
A. 240° B. 120° C. 180° D. 90°
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知点A(－1，y1)、B(2，y2)都在双曲线y＝
上，且y1＞y2，则m的取值范围是______________
若抛物线y＝x2－2x－3与x轴分别交于A，B两点，则AB的长为 ______．
查看答案直线y=x+3上有一点P(3,a)，则点P关于原点的对称点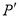为___________.
如图，两个反比例函数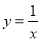和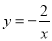的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则△PAB的面积为（ ）
A. 3 B. 4 C. 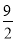D. 5
如图是二次函数y=ax2+bx+c的图象，下列结论： ①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为﹣1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案某同学在用描点法画二次函数y=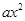+bx+c的图象时，列出了下面的表格：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣5 | … |
由于粗心，他算错了其中一个y值，则这个错误的数值是（ ）.
A．﹣11 B．﹣2 C．1 D．﹣5
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
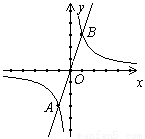
如图，反比例函数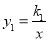
和正比例函数y2=k2x 的图象交于A（-1，-3）、B（1，3）两点，若
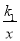＞k2x，则x的取值范围是___________________.
已知点A(－1，y1)、B(2，y2)都在双曲线y＝上，且y1＞y2，则m的取值范围是______________
若抛物线y＝x2－2x－3与x轴分别交于A，B两点，则AB的长为 ______．
查看答案直线y=x+3上有一点P(3,a)，则点P关于原点的对称点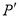为___________.
如图，两个反比例函数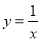和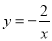的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则△PAB的面积为（ ）
A. 3 B. 4 C. 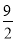D. 5
如图是二次函数y=ax2+bx+c的图象，下列结论： ①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为﹣1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案 试题属性- 题型：填空题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
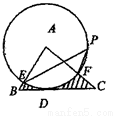
如图，在△ABC中，BC＝4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于E，交AC于F，点P是⊙A上的一点，且∠EPF＝40°，则图中阴影部分的面积是__________（结果保留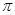
）
如图，反比例函数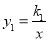和正比例函数y2=k2x 的图象交于A（-1，-3）、B（1，3）两点，若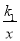＞k2x，则x的取值范围是___________________.
已知点A(－1，y1)、B(2，y2)都在双曲线y＝上，且y1＞y2，则m的取值范围是______________
若抛物线y＝x2－2x－3与x轴分别交于A，B两点，则AB的长为 ______．
查看答案直线y=x+3上有一点P(3,a)，则点P关于原点的对称点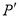为___________.
如图，两个反比例函数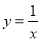和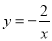的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则△PAB的面积为（ ）
A. 3 B. 4 C. 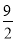D. 5
- 题型：单选题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
已知抛物线经过三点A(2,6)、B(-1,0)、C(3,0)．
求这条抛物线所对应的二次函数的解析式；
（2）写出它的对称轴和顶点坐标.
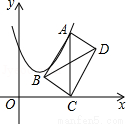
（1）y=-2x²+4x+6；（2）对称轴为x=1，顶点坐标为（1，8） 【解析】试题分析：（1）题目已知抛物线与x轴的交点坐标，故将函数解析式设为交点式，再将另一个点的坐标代入函数解析式求出解析式中的未知参数即可；（2）将函数解析式化为顶点式，写出对称轴和顶点坐标. 试题解析： 【解析】 （1）设y=a（x+1）（x－3）， 将A(2，6)代入解析式，得6=a（2+1）...如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
如图，在△ABC中，BC＝4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于E，交AC于F，点P是⊙A上的一点，且∠EPF＝40°，则图中阴影部分的面积是__________（结果保留）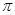
如图，反比例函数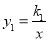和正比例函数y2=k2x 的图象交于A（-1，-3）、B（1，3）两点，若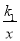＞k2x，则x的取值范围是___________________.
已知点A(－1，y1)、B(2，y2)都在双曲线y＝上，且y1＞y2，则m的取值范围是______________
若抛物线y＝x2－2x－3与x轴分别交于A，B两点，则AB的长为 ______．
查看答案 试题属性- 题型：解答题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．
（1）若他去买一瓶饮料，则他买到奶汁的概率是 ；
（2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．
(1)．(2)． 【解析】（1）∵商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同， ∴他去买一瓶饮料，则他买到奶汁的概率是： ， 故答案为：0.25 ； （2）画树状图得：(可以用字母代替) 12种情况需列举出来 ∵共有12种等可能的结果，他恰好买到雪碧和奶汁的有2种情况，(雪,奶),(奶,雪) ∴他恰...已知抛物线经过三点A(2,6)、B(-1,0)、C(3,0)．
求这条抛物线所对应的二次函数的解析式；
（2）写出它的对称轴和顶点坐标.
查看答案如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
如图，在△ABC中，BC＝4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于E，交AC于F，点P是⊙A上的一点，且∠EPF＝40°，则图中阴影部分的面积是__________（结果保留）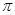
如图，反比例函数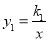和正比例函数y2=k2x 的图象交于A（-1，-3）、B（1，3）两点，若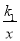＞k2x，则x的取值范围是___________________.
已知点A(－1，y1)、B(2，y2)都在双曲线y＝上，且y1＞y2，则m的取值范围是______________
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
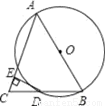
如图所示，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC于E．
（1）求证：AB=AC；
（2）求证：DE为⊙O的切线．
商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．
（1）若他去买一瓶饮料，则他买到奶汁的概率是 ；
（2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．
查看答案已知抛物线经过三点A(2,6)、B(-1,0)、C(3,0)．
求这条抛物线所对应的二次函数的解析式；
（2）写出它的对称轴和顶点坐标.
查看答案如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
如图，在△ABC中，BC＝4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于E，交AC于F，点P是⊙A上的一点，且∠EPF＝40°，则图中阴影部分的面积是__________（结果保留）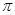
如图，反比例函数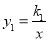和正比例函数y2=k2x 的图象交于A（-1，-3）、B（1，3）两点，若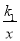＞k2x，则x的取值范围是___________________.
- 题型：解答题
- 难度：简单
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
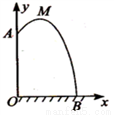
如图所示， 有一建筑工地从10m 高的窗A处用水管向外喷水，喷出的水呈抛物线状，如果抛物线的最高点M 离墙1m，离地面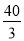
m.
（1）求抛物线的解析式；
（2）求水流落地点B离墙的距离OB.
如图所示，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC于E．
（1）求证：AB=AC；
（2）求证：DE为⊙O的切线．
商店只有雪碧、可乐、果汁、奶汁四种饮料，每种饮料数量充足，某同学去该店购买饮料，每种饮料被选中的可能性相同．
（1）若他去买一瓶饮料，则他买到奶汁的概率是 ；
（2）若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．
查看答案已知抛物线经过三点A(2,6)、B(-1,0)、C(3,0)．
求这条抛物线所对应的二次函数的解析式；
（2）写出它的对称轴和顶点坐标.
查看答案如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+4上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为____．
如图，在△ABC中，BC＝4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于E，交AC于F，点P是⊙A上的一点，且∠EPF＝40°，则图中阴影部分的面积是__________（结果保留）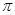
- 题型：解答题
- 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧