关于x的方程x2+kx﹣1=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
A 【解析】试题解析:Δ=k2-4×1×(-1)=k2+4 ∵k2≥0 ∴Δ=k2+4>0 ∴关于x的方程x2+kx﹣1=0有两个不相等的实数根. 故选A.如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )
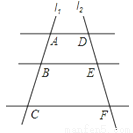
A. 4 B. 5 C. 6 D. 8
查看答案砀山果园场2015年水果产量为100吨,2017年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为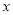 ,则根据题意可列方程为( )
,则根据题意可列方程为( )
A. 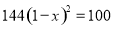 B.
B. 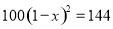
C. 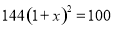 D.
D. 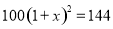
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 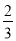 B.
B. 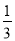 C.
C. 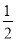 D.
D. 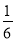
下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A. ①③ B. ②③ C. ③④ D. ①②③
查看答案如图,几何体的左视图是( )
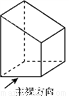

A. (A) B. (B) C. (C) D. (D)
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
C 【解析】【解析】 ∵△ABC与△DEF的相似比为1:4,∴△ABC与△DEF的周长比为1:4.故选C.关于x的方程x2+kx﹣1=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )

A. 4 B. 5 C. 6 D. 8
查看答案砀山果园场2015年水果产量为100吨,2017年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为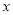 ,则根据题意可列方程为( )
,则根据题意可列方程为( )
A. 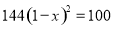 B.
B. 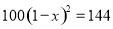
C. 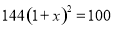 D.
D. 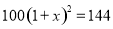
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 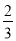 B.
B. 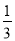 C.
C. 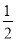 D.
D. 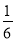
下列条件中能使平行四边形ABCD为菱形的是( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A. ①③ B. ②③ C. ③④ D. ①②③
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为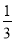 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )
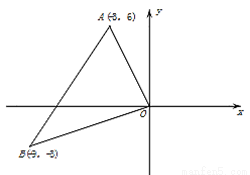
A. (-1,2) B. (-1,2)或(1,-2)
C. (-9,18)或(9,-18) D. (1,-2)
B 【解析】试题解析:∵点A(-3,6),以原点O为位似中心,相似比为,把△ABO缩小, ∴点A的对应点A′的坐标是(-1,2)或(1,-2), 故选B. 点睛:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
查看答案关于x的方程x2+kx﹣1=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )

A. 4 B. 5 C. 6 D. 8
查看答案砀山果园场2015年水果产量为100吨,2017年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为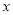 ,则根据题意可列方程为( )
,则根据题意可列方程为( )
A. 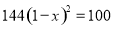 B.
B. 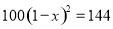
C. 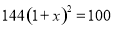 D.
D. 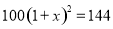
要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )
A. 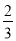 B.
B. 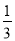 C.
C. 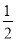 D.
D. 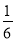
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )
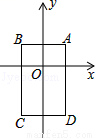
A. (-1,-2) B. (-1,1) C. (-1,-1) D. (1,-2)
D 【解析】试题解析:∵A(1,1),B(-1,1),C(-1,-2),D(1,-2), ∴AB=CD=2,AD=BC=3,且四边形ABCD为矩形, ∴矩形ABCD的周长C矩形ABCD=2(AB+BC)=10. ∵2017=201×10+7,AB+BC+CD=7, ∴细线的另一端落在点D上,即(1,-2). 故选D.如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为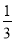 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A. (-1,2) B. (-1,2)或(1,-2)
C. (-9,18)或(9,-18) D. (1,-2)
查看答案△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
查看答案关于x的方程x2+kx﹣1=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )

A. 4 B. 5 C. 6 D. 8
查看答案砀山果园场2015年水果产量为100吨,2017年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为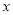 ,则根据题意可列方程为( )
,则根据题意可列方程为( )
A. 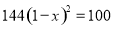 B.
B. 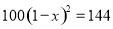
C. 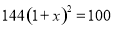 D.
D. 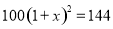
- 题型:单选题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
5 【解析】试题分析:根据根与系数的关系可知m+n=﹣2,又知m是方程的根,所以可得m2+2m﹣7=0,最后可将m2+3m+n变成m2+2m+m+n,最终可得答案. ∵设m、n是一元二次方程x2+2x﹣7=0的两个根, ∴m+n=﹣2, ∵m是原方程的根, ∴m2+2m﹣7=0,即m2+2m=7, ∴m2+3m+n=m2+2m+m+n=7﹣2=5 考点:根与系数的关系 ...如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )

A. (-1,-2) B. (-1,1) C. (-1,-1) D. (1,-2)
查看答案如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为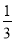 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A. (-1,2) B. (-1,2)或(1,-2)
C. (-9,18)或(9,-18) D. (1,-2)
查看答案△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
查看答案关于x的方程x2+kx﹣1=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案如图,AD∥BE∥CF,直线l1、l2与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则DF的长为( )

A. 4 B. 5 C. 6 D. 8
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
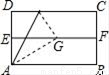
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______
设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
查看答案如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )

A. (-1,-2) B. (-1,1) C. (-1,-1) D. (1,-2)
查看答案如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为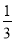 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A. (-1,2) B. (-1,2)或(1,-2)
C. (-9,18)或(9,-18) D. (1,-2)
查看答案△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
查看答案关于x的方程x2+kx﹣1=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 只有一个实数根 D. 没有实数根
查看答案 试题属性- 题型:填空题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=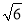 ,AD=2.当AB=_______时,△ABC与△ACD相似.
,AD=2.当AB=_______时,△ABC与△ACD相似.
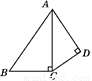
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______

设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
查看答案如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )

A. (-1,-2) B. (-1,1) C. (-1,-1) D. (1,-2)
查看答案如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为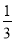 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A. (-1,2) B. (-1,2)或(1,-2)
C. (-9,18)或(9,-18) D. (1,-2)
查看答案△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为( )
A. 1:2 B. 1:3 C. 1:4 D. 1:16
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
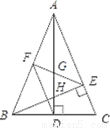
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=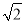 AE2;④S△ABC=4S△ADF.其中正确的有___________.
AE2;④S△ABC=4S△ADF.其中正确的有___________.
如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=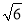 ,AD=2.当AB=_______时,△ABC与△ACD相似.
,AD=2.当AB=_______时,△ABC与△ACD相似.

如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______

设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
查看答案如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )

A. (-1,-2) B. (-1,1) C. (-1,-1) D. (1,-2)
查看答案如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为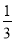 ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A. (-1,2) B. (-1,2)或(1,-2)
C. (-9,18)或(9,-18) D. (1,-2)
查看答案 试题属性- 题型:填空题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
解方程:x+5=x2-25.
x1=-5,x2=6 【解析】试题分析:移项,运用因式分解法即可求出方程的解. 试题解析:x+5=x2-25 x2-x-30=0 (x+5)(x-6)=0 x+5=0,x-6=0 x1=-5,x2=6.如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=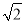 AE2;④S△ABC=4S△ADF.其中正确的有___________.
AE2;④S△ABC=4S△ADF.其中正确的有___________.

如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=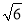 ,AD=2.当AB=_______时,△ABC与△ACD相似.
,AD=2.当AB=_______时,△ABC与△ACD相似.

如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______

设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
查看答案如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是( )

A. (-1,-2) B. (-1,1) C. (-1,-1) D. (1,-2)
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
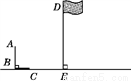
如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
解方程:x+5=x2-25.
查看答案如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=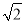 AE2;④S△ABC=4S△ADF.其中正确的有___________.
AE2;④S△ABC=4S△ADF.其中正确的有___________.

如图,在两个直角三角形中,∠ACB=∠ADC=90°,AC=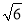 ,AD=2.当AB=_______时,△ABC与△ACD相似.
,AD=2.当AB=_______时,△ABC与△ACD相似.

如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为 _______

设m、n是一元二次方程x2+2x﹣7=0的两个根,则m2+3m+n=__.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧