0 319028 319036 319042 319046 319052 319054 319058 319064 319066 319072 319078 319082 319084 319088 319094 319096 319102 319106 319108 319112 319114 319118 319120 319122 319123 319124 319126 319127 319128 319130 319132 319136 319138 319142 319144 319148 319154 319156 319162 319166 319168 319172 319178 319184 319186 319192 319196 319198 319204 319208 319214 319222 366461
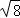 ﹣(﹣1)2.
﹣(﹣1)2.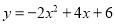 .
. 轴的交点坐标.
轴的交点坐标.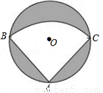
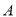 处测得灯塔
处测得灯塔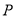 在北偏东
在北偏东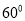 方向上,继续航行1小时到达
方向上,继续航行1小时到达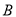 处,此时测得灯塔
处,此时测得灯塔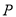 在北偏东
在北偏东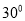 方向上.
方向上.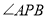 的度数;
的度数;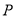 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?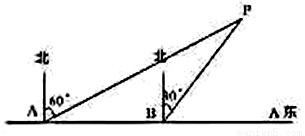
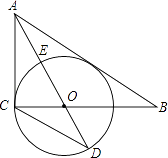
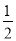 ,求
,求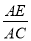 的值.
的值. 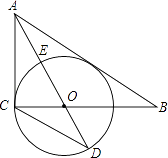
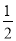 ,求
,求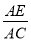 的值.
的值. 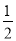 (3)
(3)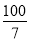
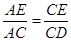 = tanD=
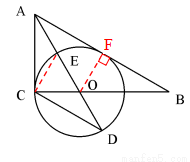
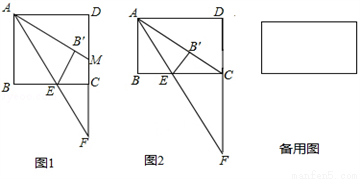
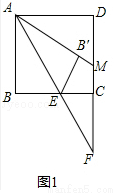
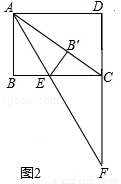
= tanD=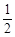 ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得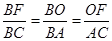 ,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
,设BO="y" ,BF=z,列二元一次方程组即可解决问题.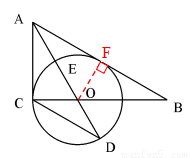
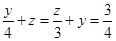
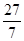 y=
y=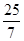
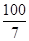
 ;(2)
;(2) .
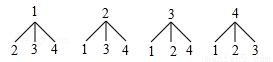
.
 =
=
 .
.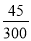 =
=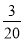 ,
,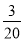 .
.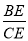 =_____;
=_____;
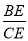 =_____;
=_____;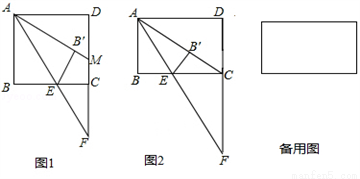
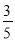 ;(3)
;(3) .
.
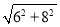 =10,
=10,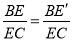 =sin∠ACB=
=sin∠ACB=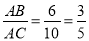 ,
,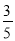 .
.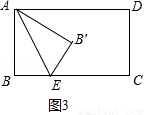
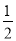 •6•x=3x,
•6•x=3x,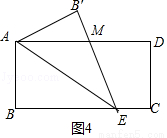
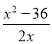 ,
,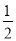 ×6×
×6×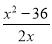 =
=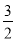 x+
x+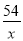 .
. .
.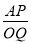 =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.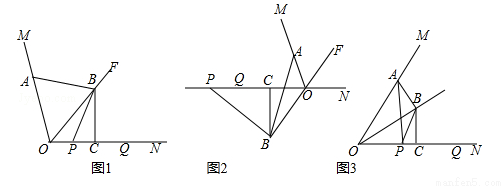
 =k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
=k,当P和Q两点都在射线ON上移动时,k是否存在最小值?若存在,请直接写出k的最小值;若不存在,请说明理由.
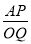 =
=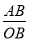 ,由∠AOB=30°,推出当BA⊥OM时,
,由∠AOB=30°,推出当BA⊥OM时, 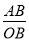 的值最小,最小值为0.5,由此即可解决问题;
的值最小,最小值为0.5,由此即可解决问题;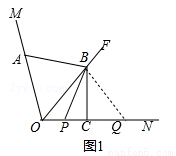
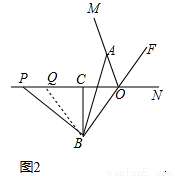
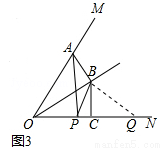
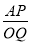 =
=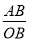 ,∵∠AOB=30°,∴当BA⊥OM时,
,∵∠AOB=30°,∴当BA⊥OM时, 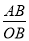 的值最小,最小值为0.5,∴k=0.5.
的值最小,最小值为0.5,∴k=0.5.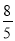 x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣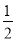 x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+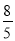 x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.