某商店计划购进一批圆规和水笔,这批商品数量之和为200,进货总价不小于190元,但不超过250元,有关销售策略与售价等信息如下表所示:
(1)求总利润y元与圆规个数x的函数关系式,并求出x的取值范围.
(2)在全部可销售完的情况下,随着a的变化,选择怎样的进货方案获得的总利润大?
| 圆规(元/个) | 水笔(元/支) | |
| 成本 | 2 | 0.5 |
| 售价 | a(2<a<3且a≠2.5) | 1 |
某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格:
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
落在“铅笔”的频率 |
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?(精确到1°)

 -
-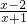 )÷
)÷ ,其中x满足x2-x-1=0.
,其中x满足x2-x-1=0. 数关系如下图所示:
数关系如下图所示: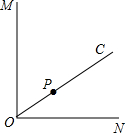 如图,已知OM⊥ON,垂足为点O,点P是射线OC上一点.
如图,已知OM⊥ON,垂足为点O,点P是射线OC上一点. 的中点.
的中点. 如图,以BC为直径,在半径为2,圆心角为90°的扇形内作半圆,交弦AB于点D,连接CD,求图中阴影部分的面积.
如图,以BC为直径,在半径为2,圆心角为90°的扇形内作半圆,交弦AB于点D,连接CD,求图中阴影部分的面积.