题目内容
解答下列各题：
（1）计算：计算：
（2）先化简，再求值：（
-
）÷
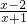，其中x满足x2-x-1=0．
解：（1）原式=3-1+4
-
=2+3；
（2）原式=
÷
=
×
=
，
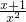∵x满足x2-x-1=0，
∴x2=x+1，
∴原式=
=1．
分析：（1）先分别根据负整数指数幂、0指数幂、绝对值的性质及特殊角的三角函数值计算出各数，再根据实数混合运算的法则进行计算即可；
（2）先根据分式混合运算的法则把原式进行化简，再根据x满足x2-x-1=0得出x2的表达式，代入原式进行计算即可．
点评：本题考查的是分式的化简求值及实数的运算，熟知分式混合运算的法则，负整数指数幂、0指数幂、绝对值的性质及特殊角的三角函数值是解答此题的关键．
-=2+3
；（2）原式=
÷=
×=
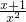，∵x满足x2-x-1=0，
∴x2=x+1，
∴原式=
=1．分析：（1）先分别根据负整数指数幂、0指数幂、绝对值的性质及特殊角的三角函数值计算出各数，再根据实数混合运算的法则进行计算即可；
（2）先根据分式混合运算的法则把原式进行化简，再根据x满足x2-x-1=0得出x2的表达式，代入原式进行计算即可．
点评：本题考查的是分式的化简求值及实数的运算，熟知分式混合运算的法则，负整数指数幂、0指数幂、绝对值的性质及特殊角的三角函数值是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
