4．
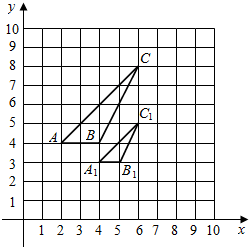如图，△ABC与△A1B1C1是位似图形，且顶点都在格点上，则位似中心坐标是（ ）
如图，△ABC与△A1B1C1是位似图形，且顶点都在格点上，则位似中心坐标是（ ）| A． | （6，2） | B． | （6，1） | C． | （4，2） | D． | （2，6） |
3．某厂工人小王某月工作的部分信息如下：
信息一：工作时间：每天上午8：00～12：00，下午13：00～17：00，每月25天；
信息二：生产甲、乙两种产品，并且按规定每月生产甲产品的件数不少于60件．
生产产品的件数与所用时间之间的关系如下表：
信息三：按件计酬，每生产一件甲产品可得1.5元，每生产一件乙产品可得2.80元．
根据以上信息，回答下列问题：
（1）小王每生产一件甲种产品，每生产一件乙种产品分别需要多少分钟？
（2）若小王每月生产甲产品a件，乙产品b件，当a、b分别是多少时，小王收入最多？
信息一：工作时间：每天上午8：00～12：00，下午13：00～17：00，每月25天；
信息二：生产甲、乙两种产品，并且按规定每月生产甲产品的件数不少于60件．
生产产品的件数与所用时间之间的关系如下表：
| 生产甲产品件数（件） | 生产乙产品件数（件） | 所用总时间（min） |
| 10 | 10 | 350 |
| 30 | 20 | 850 |
根据以上信息，回答下列问题：
（1）小王每生产一件甲种产品，每生产一件乙种产品分别需要多少分钟？
（2）若小王每月生产甲产品a件，乙产品b件，当a、b分别是多少时，小王收入最多？
12．多项式的乘法法则知：若（x+a）（x+b）=x2+px+q，则p=a+b，q=a•b；反过来x2+px+q=（x+a）（x+b），要将多项式x2+px+q进行分解，关键是找到两个数a、b，使a+b=p，a•b=q，如对多项式x2-3x+2，有p=-3，q=2，a=-1，b=-2，此时（-1）+（-2）=-3，（-1）（-2）=2，所以x2-3x+2可分解为（x-1）（x-2），即x2-3x+2=（x-1）（x-2）
（1）根据以上填写下表：
（2）根据填表，还可得出如下结论：当q是正数时，应分解成两个因数a、b同号，a、b的符号与p相同；当q为负数时，应分解成的两个因数a、b异号，a、b中绝对值较大的因数的符合与p相同．
（3）分解因式x2-x-12=（x-4）（x+3）；x2-7x+6=（x-1）（x-6）．
0 312990 312998 313004 313008 313014 313016 313020 313026 313028 313034 313040 313044 313046 313050 313056 313058 313064 313068 313070 313074 313076 313080 313082 313084 313085 313086 313088 313089 313090 313092 313094 313098 313100 313104 313106 313110 313116 313118 313124 313128 313130 313134 313140 313146 313148 313154 313158 313160 313166 313170 313176 313184 366461
（1）根据以上填写下表：
| 多项式 | p | q | a | b | 分解结果 |
| x2+9x+20 | 9 | 20 | 4 | 5 | （x+4）（x+5） |
| x2-9x+20 | -9 | 20 | -4 | -5 | （x-4）（x-5） |
（3）分解因式x2-x-12=（x-4）（x+3）；x2-7x+6=（x-1）（x-6）．