15. 如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
0 311615 311623 311629 311633 311639 311641 311645 311651 311653 311659 311665 311669 311671 311675 311681 311683 311689 311693 311695 311699 311701 311705 311707 311709 311710 311711 311713 311714 311715 311717 311719 311723 311725 311729 311731 311735 311741 311743 311749 311753 311755 311759 311765 311771 311773 311779 311783 311785 311791 311795 311801 311809 366461
 如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )
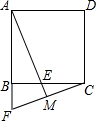
如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( )| A. | BE=CE | B. | FM=MC | C. | AM⊥FC | D. | BF⊥CF |
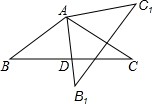 已知,如图,在△ABC中,AB=AC,AD是BC边上的中线,将△ABC绕点A按逆时针方向旋转,边AB落在直线AD上得到△AB1C1,求证:B1C1⊥AC.
已知,如图,在△ABC中,AB=AC,AD是BC边上的中线,将△ABC绕点A按逆时针方向旋转,边AB落在直线AD上得到△AB1C1,求证:B1C1⊥AC. 如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.
如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.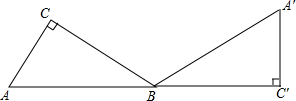 如图,Rt△ABC中,∠C=90°,AB=4,AC=2,将△ABC顺时针旋转至△A′BC′的位置上,使点A,B,C′三点在同一条直线上,则旋转中心是哪一点?旋转角为多少度?
如图,Rt△ABC中,∠C=90°,AB=4,AC=2,将△ABC顺时针旋转至△A′BC′的位置上,使点A,B,C′三点在同一条直线上,则旋转中心是哪一点?旋转角为多少度?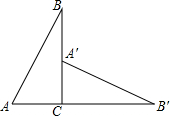 如图所示在△ABC中,∠ACB=90°,△CA′B′是由△ABC绕顶点C旋转得到的,且A,C,B′三点在同一直线上,那么A′B′与AB的关系怎样?试说明理由.
如图所示在△ABC中,∠ACB=90°,△CA′B′是由△ABC绕顶点C旋转得到的,且A,C,B′三点在同一直线上,那么A′B′与AB的关系怎样?试说明理由.
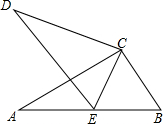 如图,将Rt△ABC绕直角顶点C顺时针旋转一定的角度到△DEC的位置,若E点在AB边上,且∠DCB=160°,则∠AED=70°.
如图,将Rt△ABC绕直角顶点C顺时针旋转一定的角度到△DEC的位置,若E点在AB边上,且∠DCB=160°,则∠AED=70°.