作出一次函数y=2x+2的图象．

已知点（x₁，-1）、（x₂，-）、（x₃，2）在函数y=-的图象上，下列关系式中，正确的

1. A.
   x₁＞x₂＞x₃
2. B.
   x₃＞x₂＞x₁
3. C.
   x₂＞x₁＞x₃
4. D.
   x₃＞x₁＞x₂

已知：点P（a，2）关于x轴的对称点在反比例函数y=-（x＞0）的图象上，y关于x的函数y=（1-a）x+3的图象交x轴于点A﹑交y轴于点B．求点P坐标和△PAB的面积．

正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，设格点多边形各边上的格点的个数和为a，格点边多边形内部的格点个数和为b，格点多边形的面积为S，图l、图2是两个格点多边形．
（1）根据图中提供的信息填表：

一般格点多边形	a	b	a+2b	S
多边形1（图1）	6	1	______	______
多边形2（图2）	7	2	11	______
…	…	…	…	…

（2）在给定的正三角形网格中分别画出一个面积为3、4、5的格点多边形：
（3）猜想S与a、b之间的关系：S=______（用含a、b的代数式表示）；
（4）若一个格点多边形的面积为S，b是否存在最大值和最小值？若存在求出最大值和最小值；若不存在，请说明理由．

如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．
（1）试找出一个与△AED全等的三角形，并加以证明．
（2）若AB=8，DE=3，P为线段AC上的任意一点，PG⊥AE于G，PH⊥EC于H，PG+PH的值会变化吗？若变化，请说明理由； 若不变化，请求出这个值．

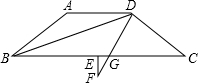如图，等腰梯形ABCD，AD∥BC，AB=CD，BD平分∠ABC，点E为BC中点，EF⊥BC，DF=DC，DF交BC于点G，若EG=1，BE=9，则AD=________．

将一副三角尺如图所示放置，则∠α与∠β的数量关系是________．

计算：234²-468×134+134²=________．

如图，点A、C、B在同一直线上，△DAC和△EBC均是等边三角形，AE与BD交于点O，AE、BD分别与CD、CE交于点M、N，有如下结论：①AE=BD；②△ACM≌△DCN；③EM=BN；④MN∥BC；⑤∠DOA=60°，其中，正确的结论个数是

1. A.
   5个
2. B.
   4个
3. C.
   3个
4. D.
   2个

如图，某地有两所大学A、B和两条相交叉的公路l₁、l₂，现计划修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等．你能确定仓库应该建在什么位置吗？在所给的图形中画出你的设计方案．（不写已知、求作、作法，只保留作图痕迹）