4.使分式$\frac{a+1}{a-1}$有意义的a的取值范围为( )
| A. | a<1 | B. | a>1 | C. | a≠1 | D. | a=1 |
2.如果点A位于第三象限,且点A到x轴的距离为3,点A到y轴的距离为4,那么点A的坐标为( )
| A. | (-3,-4) | B. | (-4,-3) | C. | (3,-4) | D. | (-4,3) |
1. 如图,在学校某处建立平面直角坐标系,使得教学楼位于(0,0),实验楼位于(-2,2),那么食堂位于( )
如图,在学校某处建立平面直角坐标系,使得教学楼位于(0,0),实验楼位于(-2,2),那么食堂位于( )
 如图,在学校某处建立平面直角坐标系,使得教学楼位于(0,0),实验楼位于(-2,2),那么食堂位于( )
如图,在学校某处建立平面直角坐标系,使得教学楼位于(0,0),实验楼位于(-2,2),那么食堂位于( )| A. | (2,4) | B. | (2,3) | C. | (3,3) | D. | (3,4) |
20. 如图,点P的坐标为( )
如图,点P的坐标为( )
 如图,点P的坐标为( )
如图,点P的坐标为( )| A. | (1,2) | B. | (2,-1) | C. | (-1,2) | D. | (-1,-2) |
19.已知命题:①若n<1,则n2<1;②一个锐角小于这个角的补角,则下列说法正确的是( )
| A. | ①的条件是n2<1 | B. | ①是真命题 | ||
| C. | ②的条件是如果一个角是锐角 | D. | ②是假命题 |
18.一张正方形的纸片,如图1进行两次对折,折成一个正方形,从右下角的顶点,沿斜虚线剪去一个角剪下的实际是四个小三角形,再把余下的部分展开,展开后的这个图形的内角和是多少度?( )


| A. | 1080° | B. | 360° | C. | 180° | D. | 900° |
17.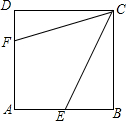 如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
 如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )| A. | 4 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |
16.下列说法中错误的是( )
| A. | x轴上所有点的纵坐标都相等 | |
| B. | y轴上的所有点的横坐标都相等 | |
| C. | 原点的坐标是(0,0) | |
| D. | 坐标分别为(-1,2)与(2,-1)的点是同一个点 |
15. 盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒中摇匀再摸球.在活动中得到如表中部分数据.
盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒中摇匀再摸球.在活动中得到如表中部分数据.
(1)请将表中数据补充完整,a=90;b=30.5%;c=29.8%
(2)画出“出现红球”的频率折线统计图,观察所画折线图,你发现了什么?
(3)如果从盒内摸出一球,你认为盒内哪种颜色的球多?摸到白球的概率有多大?
0 285870 285878 285884 285888 285894 285896 285900 285906 285908 285914 285920 285924 285926 285930 285936 285938 285944 285948 285950 285954 285956 285960 285962 285964 285965 285966 285968 285969 285970 285972 285974 285978 285980 285984 285986 285990 285996 285998 286004 286008 286010 286014 286020 286026 286028 286034 286038 286040 286046 286050 286056 286064 366461
 盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒中摇匀再摸球.在活动中得到如表中部分数据.
盒子里装有红球和白球共10个,它们除颜色外其他都相同,每次从盒子里摸出1个球,记下颜色后放回盒中摇匀再摸球.在活动中得到如表中部分数据. | 摸球次数 | 出现红球的频数 | 出现红球的频率 | 摸球次数 | 出现红球的频数 | 出现红球的频率 |
| 100 | 32 | 32% | 400 | 122 | b |
| 200 | 62 | 31% | 500 | 149 | c |
| 300 | a | 30% | 600 | 183 | 30.5% |
(2)画出“出现红球”的频率折线统计图,观察所画折线图,你发现了什么?
(3)如果从盒内摸出一球,你认为盒内哪种颜色的球多?摸到白球的概率有多大?