13.若$\frac{a}{b}=\frac{c}{d}=\frac{1}{2}(b≠d)$,则下列式子不正确的是( )
| A. | $\frac{a+b}{b}=\frac{3}{2}$ | B. | $\frac{a+2c}{b+2d}=2$ | C. | $\frac{a-c}{b-d}=\frac{1}{2}$ | D. | b=2a |
12.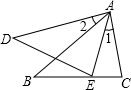 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )| A. | ∠C=∠AED | B. | $\frac{AB}{AD}=\frac{AC}{AE}$ | C. | ∠B=∠D | D. | $\frac{AB}{AD}=\frac{BC}{DE}$ |
11.2011年成都市大约有3万名学生参加中考,为了考查他们的数学考试情况,评卷人抽取了1000名学生的数学成绩进行统计,那么下列四个判断正确的是( )
| A. | 每名学生的数学成绩是个体 | B. | 3万名学生是总体 | ||
| C. | 上述调查是普查 | D. | 1000名考生是总体的一个样本 |
10.下列分解因式结果正确的是( )
| A. | y3-y=y(y2-1) | B. | x2-x-3=x(x-1)-3 | C. | -m2+n2=-(m-n)(m+n) | D. | x2-3x+9=(x-3)2 |
9.当x=1时,下列各式的值为0的是( )
| A. | $\frac{x-1}{{{x^2}-3x+2}}$ | B. | $\frac{1}{x+1}$ | C. | $\frac{2x-2}{x-2}$ | D. | $\frac{x+2}{x-1}$ |
6.1号探测气球从海拔5米处出发,以1米/分的速度上升.与此同时,2号探测气球从海拔15米处出发,以0.5米/分的速度上升,两个气球都匀速上升了50分钟.
设气球球上升时间为x分(0≤x≤50)
(1)根据题意,填写下表:
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由;
(3)当两个气球所在位置的海拔相差7.5米时,这时气球上升了多长时间?
0 281257 281265 281271 281275 281281 281283 281287 281293 281295 281301 281307 281311 281313 281317 281323 281325 281331 281335 281337 281341 281343 281347 281349 281351 281352 281353 281355 281356 281357 281359 281361 281365 281367 281371 281373 281377 281383 281385 281391 281395 281397 281401 281407 281413 281415 281421 281425 281427 281433 281437 281443 281451 366461
设气球球上升时间为x分(0≤x≤50)
(1)根据题意,填写下表:
| 上升时间/分 | 10 | 30 | … | x |
| 1号探测气球所在位置的海拔/米 | 15 | 35 | … | x+5 |
| 2号探测气球所在位置的海拔/米 | 20 | 30 | … | 0.5x+15 |
(3)当两个气球所在位置的海拔相差7.5米时,这时气球上升了多长时间?
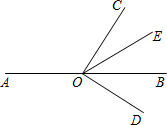 如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.
如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.