0 266548 266556 266562 266566 266572 266574 266578 266584 266586 266592 266598 266602 266604 266608 266614 266616 266622 266626 266628 266632 266634 266638 266640 266642 266643 266644 266646 266647 266648 266650 266652 266656 266658 266662 266664 266668 266674 266676 266682 266686 266688 266692 266698 266704 266706 266712 266716 266718 266724 266728 266734 266742 366461
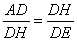 ,即
,即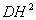 =AD×DE.
=AD×DE.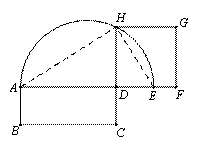
 +2,求AB.
+2,求AB.



 ;
;  ,其中x=2.
,其中x=2.