在平面直角坐标系 中,
中, 的半径为r,P是与圆心C不重合的点,点P关于
的半径为r,P是与圆心C不重合的点,点P关于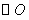 的反称点的定义如下:若
的反称点的定义如下:若 在射线CP上存在一点
在射线CP上存在一点 ,满足
,满足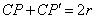 ,则称
,则称 为点P关于
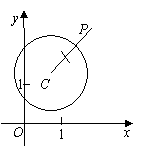
为点P关于 的反称点,下图为点P及其
的反称点,下图为点P及其 关于
关于 的反称点
的反称点 的示意图。
的示意图。
 |
(1)当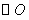 的半径为1时。
的半径为1时。
①分别判断点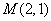 ,
,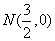 ,
,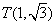 关于
关于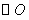 的反称点是否存在,若存
的反称点是否存在,若存 在?
在?
求其坐标;
②点P在直线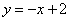 上,若点P关于
上,若点P关于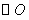 的反称点
的反称点 存在,且点
存在,且点 不在x轴上,求点P的横坐标的取值范围;
不在x轴上,求点P的横坐标的取值范围;
(2)当 的圆心在x轴上,半径为1,直线
的圆心在x轴上,半径为1,直线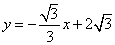 与x轴,y轴分别交于点A,B,若线段AB上存在点P,使得点P关于
与x轴,y轴分别交于点A,B,若线段AB上存在点P,使得点P关于 的反称点
的反称点 在
在 的内部,求圆心C的横坐标的取值范围。
的内部,求圆心C的横坐标的取值范围。
有这样一个问题:探究函数 的图象与性质。
的图象与性质。
小东根据学习函数的经验,对函数 的图象与性质进行了探究。
的图象与性质进行了探究。
下面是小东的探究过程,请补充完成:
(1)函数 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
(2)下表是y与x的几组对应值。
| x | … |
|
|
|
|
|
|
| 1 | 2 | 3 | … |
| y | … |
|
|
|
|
|
|
|
|
| m | … |
求m的值;
 (3)如下图,在平面直角坐标系
(3)如下图,在平面直角坐标系 中,描出了以上表中各对对应值为坐标的点,格局描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,格局描出的点,画出该函数的图象;
 (4)进一步探究发现,该函数图象在第一象限内的最低点
(4)进一步探究发现,该函数图象在第一象限内的最低点 的
的 坐标是
坐标是 ,结合函数的图象,写出该函数的其他性质(一条即可):________________。
,结合函数的图象,写出该函数的其他性质(一条即可):________________。
 ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
 ,使点D移动到点C,得到
,使点D移动到点C,得到 ,过点Q作
,过点Q作 于H,连接AH,PH。
于H,连接AH,PH。 ,正方形ABCD的边长为1,请写出求DP长的思路。(可以不写出计算结果)
,正方形ABCD的边长为1,请写出求DP长的思路。(可以不写出计算结果)
 且平行于x轴的直线,与直线
且平行于x轴的直线,与直线 交于点A,点A关于直线
交于点A,点A关于直线 的对称点为B,抛物线
的对称点为B,抛物线 经过点A,B。
经过点A,B。 的表达式及顶点坐标;
的表达式及顶点坐标; 与线段AB恰有一个公共
与线段AB恰有一个公共 点,结合函数的图象,求a的取值范围。
点,结合函数的图象,求a的取值范围。













 植物园的桃花受到了游客的热捧,两公园的
植物园的桃花受到了游客的热捧,两公园的 园林的厚重文化底蕴与满园春色成为游客的重要目的地,游客接待量分别为26万人次,17.6万人次;北京动物园游客接待量为18万人次,熊猫馆的游客密集度较高。
园林的厚重文化底蕴与满园春色成为游客的重要目的地,游客接待量分别为26万人次,17.6万人次;北京动物园游客接待量为18万人次,熊猫馆的游客密集度较高。 接待量为___________万人次。
接待量为___________万人次。 ,交AB于点F,且
,交AB于点F,且 ,链接AC,AD,延长AD交BM地点E。
,链接AC,AD,延长AD交BM地点E。 是等边三角形。
是等边三角形。 ,求OE的长。
,求OE的长。