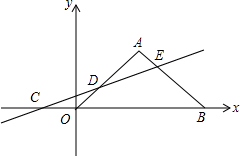
 如图,△AOB是等腰三角形,且∠A=90°,点B坐标为(6,0),过点C(-3,0)作直线L交AO于点D,交AB于点E,且△ADE和△DCO的面积相等.
如图,△AOB是等腰三角形,且∠A=90°,点B坐标为(6,0),过点C(-3,0)作直线L交AO于点D,交AB于点E,且△ADE和△DCO的面积相等.(1)求点E的坐标;
(2)求直线L的函数解析式.
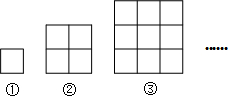 如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )
如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )| A、55 | B、78 | C、91 | D、140 |
 如图,△AOB是等腰三角形,且∠A=90°,点B坐标为(6,0),过点C(-3,0)作直线L交AO于点D,交AB于点E,且△ADE和△DCO的面积相等.
如图,△AOB是等腰三角形,且∠A=90°,点B坐标为(6,0),过点C(-3,0)作直线L交AO于点D,交AB于点E,且△ADE和△DCO的面积相等. 如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )
如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )| A、55 | B、78 | C、91 | D、140 |