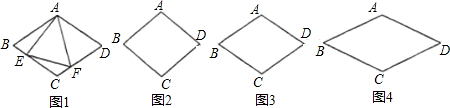
在菱形ABCD中,AB=4,∠BAD=θ,△AEF为正三角形,E、F在菱形边上.
(1)如图1,当θ=120°时,证明:不论E、F在BC、CD上如何移动,总有BE=CF.
(2)在(1)的条件下,当点E、F在BC、CD上移动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出其最大(小)值.
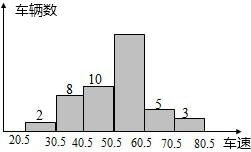
(3)操作探索:当θ分别满足下列条件时,能否作出菱形的内接正三角形AEF(E、F分别在菱形边上)?请填写下表(不必说明理由).
| 满足的条件 | 60°<θ<120° | θ=120° | 120°<θ<180° |
| 内接正△AEF个数 |

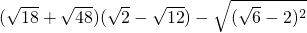 .
. 如图,△ABC的顶点A、B、C都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形,试在方格纸上按下列要求画格点三角形:
如图,△ABC的顶点A、B、C都在小正方形的顶点上,像△ABC这样的三角形叫格点三角形,试在方格纸上按下列要求画格点三角形: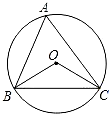 如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠A=60°,则BC的长为________.
如图,⊙O是△ABC的外接圆,连接OB、OC,若⊙O的半径为2,∠A=60°,则BC的长为________. 过第二象限,则直线y=kx-3过第
过第二象限,则直线y=kx-3过第