(本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在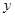 轴和
轴和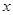 轴上,
轴上, ∠ABO=
∠ABO= .
.
【小题1】(1)求此二次函数的解析式;(4分)
【小题2】
|
 作
作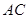 ∥
∥ 交上述函数图像于点
交上述函数图像于点 ,点
,点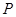 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点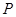 的坐标.(8分)
的坐标.(8分) (本题满分12分)
如图, 的顶点A、B在二次函数
的顶点A、B在二次函数 的图像上,又点A、B[来分别在
的图像上,又点A、B[来分别在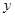 轴和
轴和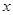 轴上,
轴上, ∠ABO=
∠ABO= .
.
【小题1】(1)求此二次函数的解析式;(4分)
【小题2】
|
 作
作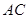 ∥
∥ 交上述函数图像于点
交上述函数图像于点 ,点
,点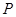 在上述函数图像上,当
在上述函数图像上,当 与
与 相似时,求点
相似时,求点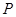 的坐标.(8分)
的坐标.(8分)