阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
(1)分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
(2)归纳:考察点的个数和可连成直线的条数 发现:如下表
发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1= |
| 3 | 3=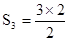 |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |  |

(4)结论:

试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数
 ,发现:(填下表)
,发现:(填下表)| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n | |
 中,
中, 厘米,
厘米, 厘米,点
厘米,点 为
为 的中点.
的中点. 与
与 是否全等,请说明理由;
是否全等,请说明理由;

 和
和 的距离.
的距离.
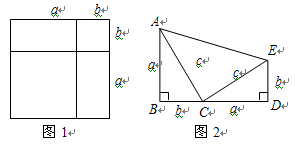
 中,
中, ,点
,点 在线段
在线段 上运动(D不与B、C重合),连接AD,作
上运动(D不与B、C重合),连接AD,作 ,
, 交线段
交线段 于
于 .
.
 时,
时, °,
°, °;点D从B向C运动时,
°;点D从B向C运动时, 逐渐变 (填“大”或“小”);
逐渐变 (填“大”或“小”); 等于多少时,
等于多少时, ≌
≌ ,请说明理由;
,请说明理由; 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出

 ,
, ,且
,且 三点共线.
三点共线. ;
;

 前
前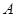 处时,他看自己的脚在镜中的像的俯角为
处时,他看自己的脚在镜中的像的俯角为 ;如果小华向后退0.5米到
;如果小华向后退0.5米到 处,这时他看自己的脚在镜中的像的俯角为
处,这时他看自己的脚在镜中的像的俯角为 .求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据: )
)