题目内容
19.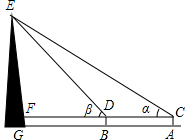 如图,小嘉利用测角仪测量塔高,他分别站在A、B两点测得塔顶的仰角α=45°,β=50°.AB为10米.已知小嘉的眼睛距地面的高度AC为1.5米,计算塔的高度.(参考数据:sin50°取0.8,cos50°取0.6,tan50°取1.2)
如图,小嘉利用测角仪测量塔高,他分别站在A、B两点测得塔顶的仰角α=45°,β=50°.AB为10米.已知小嘉的眼睛距地面的高度AC为1.5米,计算塔的高度.(参考数据:sin50°取0.8,cos50°取0.6,tan50°取1.2)
分析 设EF=x米,在Rt△FCE中,∠FCE=∠FEC=45°,可得出FC=EF,FD=x-10,在Rt△FBE中利用锐角三角函数的定义即可求出x的值,进而可得出结论.
解答 解:如图,依题意,可得CD=AB=10,FG=AC=1.5,∠EFC=90°,
在Rt△EFD中,∵β=50°,$tanβ=\frac{EF}{FD}=1.2$,
∴EF=1.2FD,
在Rt△EFC中,∵α=45°,
∴CF=EF=1.2FD,
∵CD=CF-FD=10,
∴FD=50,
∴EF=1.2FD=60,
∴EG=EF+FG=60+1.5=61.5
答:塔的高度为61.5米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
14.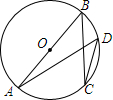 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
 如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )
如图,AB是⊙O的直径,C、D是圆上的两点.若BC=8,$cosD=\frac{2}{3}$,则AB的长为( )| A. | $\frac{{8\sqrt{13}}}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{{24\sqrt{5}}}{5}$ | D. | 12 |
 如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD交于点G,求DF:GB的值.
如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD交于点G,求DF:GB的值.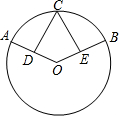 如图,在⊙O中,点C是$\widehat{AB}$的中点,D、E分别是半径OA和OB的中点,求证:CD=CE.
如图,在⊙O中,点C是$\widehat{AB}$的中点,D、E分别是半径OA和OB的中点,求证:CD=CE.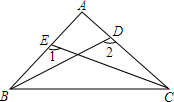 如图,已知BD=CE,∠1=∠2,求证:AB=AC.
如图,已知BD=CE,∠1=∠2,求证:AB=AC.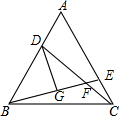 已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证:
已知,如图,在等边三角形ABC中,点D,E分别在AB,AC边上,AD=CE,CD与BE交于F,DG⊥BE,求证: