题目内容
 如图的平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
如图的平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).(1)将三角形ABC三个顶点的横坐标都减去6,分别得到A1、B1、C1,依次连接A1,B1,C1,各点,请写出A1、B1、C1的坐标并画出△A1B1C1,并判断所得三角形A1B1C1与三角形ABC的大小、形状和位置有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去5,分别得到A2、B2、C2,依次连接A2,B2,C2,各点,请写出A2、B2、C2的坐标并画出△A2B2C2,并判断所得三角形A2B2C2与三角形ABC的大小、形状和位置有什么关系?
(3)求△A2B2C2的面积.
分析:(1)在坐标系内画出△ABC与△A1B1C1,再写出A1、B1、C1的坐标即可;
(2)画出△A2B2C2,再写出A2、B2、C2的坐标即可;
(3)根据三角形的面积公式得出△A2B2C2的面积即可.
(2)画出△A2B2C2,再写出A2、B2、C2的坐标即可;
(3)根据三角形的面积公式得出△A2B2C2的面积即可.
解答: 解:(1)如图所示:
解:(1)如图所示:
A1(-2,3),B1(-3,1),C1(-5,2),
所得三角形与原三角形的大小、形状完全相同,所得三角形可看作将原三角形向左平移6个单位长度得到;
(2)如图所示,A2(4,-2),B2(3,-4),C2(1,-3),所得三角形与原三角形的大小、形状完全相同,所得三角形可看作将原三角形向下平移5个单位长度得到;
(3)∵A2B22=B2C22=5,A2C22=10,
∴△A2B2C2是等腰直角三角形,
∴S△A2B2C2=
×
×
=
.
 解:(1)如图所示:
解:(1)如图所示:A1(-2,3),B1(-3,1),C1(-5,2),
所得三角形与原三角形的大小、形状完全相同,所得三角形可看作将原三角形向左平移6个单位长度得到;
(2)如图所示,A2(4,-2),B2(3,-4),C2(1,-3),所得三角形与原三角形的大小、形状完全相同,所得三角形可看作将原三角形向下平移5个单位长度得到;
(3)∵A2B22=B2C22=5,A2C22=10,
∴△A2B2C2是等腰直角三角形,
∴S△A2B2C2=
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
点评:本题考查的是平移变换,熟知平移后的图形与原图形的大小、形状完全相同是解答此题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高
 将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD.
将边长为4的正方形在如图的平面直角坐标系中.点P是OA上的一个动点,且从点O向点A运动.连接CP交对角线OB于点D,连接AD. 在如图的平面直角坐标系中,依次描出下列各点:
在如图的平面直角坐标系中,依次描出下列各点: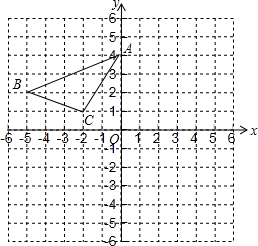 △ABC在如图的平面直角坐标系中,将其平移得到△A'B'C',若B的对应点B′的坐标为(1,1);
△ABC在如图的平面直角坐标系中,将其平移得到△A'B'C',若B的对应点B′的坐标为(1,1);