题目内容
(2013•常州)在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=
的图象上,连接OA、OB,若OA⊥OB,OB=
OA,则k=
| 1 |
| x |
| k |
| x |
| ||
| 2 |
-
| 1 |
| 2 |
-
.| 1 |
| 2 |
分析:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,设点A的坐标为(a,
),点B的坐标为(b,
),判断出△OBF∽△AOE,利用对应边成比例可求出k的值.
| 1 |
| a |
| k |
| b |
解答: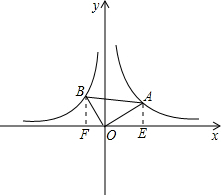 解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
设点A的坐标为(a,
),点B的坐标为(b,
),
∵∠AOE+∠BOF=90°,∠OBF+∠BOF=90°,
∴∠AOE=∠OBF,
又∵∠BFO=∠OEA=90°,
∴△OBF∽△AOE,
∴
=
=
,即
=
=
,
则
=-
b①,a=
②,
①×②可得:-2k=1,
解得:k=-
.
故答案为:-
.
 解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,设点A的坐标为(a,
| 1 |
| a |
| k |
| b |
∵∠AOE+∠BOF=90°,∠OBF+∠BOF=90°,
∴∠AOE=∠OBF,
又∵∠BFO=∠OEA=90°,
∴△OBF∽△AOE,
∴
| AE |
| OF |
| OE |
| BF |
| AO |
| OB |
| ||
| -b |
| a | ||
|
| 2 |
则
| 1 |
| a |
| 2 |
| ||
| b |
①×②可得:-2k=1,
解得:k=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了反比例函数的综合题,涉及了相似三角形的判定与性质,反比例函数图象上点的坐标的特点,解答本题要求同学们能将点的坐标转化为线段的长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•常州)在Rt△ABC中,∠C=90°,AC=1,BC=
(2013•常州)在Rt△ABC中,∠C=90°,AC=1,BC=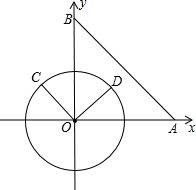 (2013•常州)在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
(2013•常州)在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.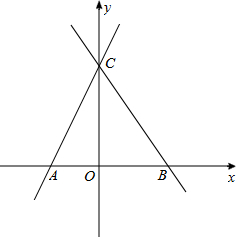 (2013•常州)在平面直角坐标系xOy中,一次函数y=2x+2的图象与x轴交于A,与y轴交于点C,点B的坐标为(a,0),(其中a>0),直线l过动点M(0,m)(0<m<2),且与x轴平行,并与直线AC、BC分别相交于点D、E,P点在y轴上(P点异于C点)满足PE=CE,直线PD与x轴交于点Q,连接PA.
(2013•常州)在平面直角坐标系xOy中,一次函数y=2x+2的图象与x轴交于A,与y轴交于点C,点B的坐标为(a,0),(其中a>0),直线l过动点M(0,m)(0<m<2),且与x轴平行,并与直线AC、BC分别相交于点D、E,P点在y轴上(P点异于C点)满足PE=CE,直线PD与x轴交于点Q,连接PA.