题目内容
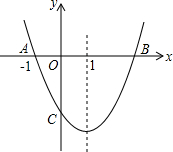 如图,抛物线y=ax2+bx+c 交x轴于A、B两点,交y轴于点C,对称轴为直线x=1,已知:A(-1,0)、C(0,-3).
如图,抛物线y=ax2+bx+c 交x轴于A、B两点,交y轴于点C,对称轴为直线x=1,已知:A(-1,0)、C(0,-3).(1)求抛物线y=ax2+bx+c 的解析式;
(2)求△AOC和△BOC的面积比;
(3)若点P在对称轴上,求AP+CP的最小值.
考点:待定系数法求二次函数解析式,二次函数的性质,轴对称-最短路线问题
专题:
分析:(1)根据交点式得出y=a(x-3)(x+1),将C(0,-3)代入求出a即可得出这条抛物线所对应的函数关系式;
(2)根据面积公式即可求得.
(3)根据抛物线的对称性求出点B的坐标,作直线BC,由几何知识可知,PA+PC=PB+PC为最小,然后根据勾股定理求得.
(2)根据面积公式即可求得.
(3)根据抛物线的对称性求出点B的坐标,作直线BC,由几何知识可知,PA+PC=PB+PC为最小,然后根据勾股定理求得.
解答:解:(1)∵对称轴为x=1,且抛物线经过A(-1,0),
∴点B(3,0),
设y=a(x-3)(x+1),把C(0,-3)代入
解得:a=1,
故解析式为:y=x2-2x-3;
(2)依题意,得OA=1,OB=3,
∴S△AOC:S△BOC=
OA•OC:
OB•OC=OA:OB
=1:3.

(3)如图,连接BC,交对称轴于点P,连接AP
∵点A关于对称轴x=1的对称点是点B(3,0)
∴由几何知识可知,PA+PC=PB+PC为最小.
在RT△BOC中,OC=3,OB=3;
∴BC=
=3
;
∴AP+CP的最小值为 3
.
∴点B(3,0),
设y=a(x-3)(x+1),把C(0,-3)代入
解得:a=1,
故解析式为:y=x2-2x-3;
(2)依题意,得OA=1,OB=3,
∴S△AOC:S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
=1:3.

(3)如图,连接BC,交对称轴于点P,连接AP
∵点A关于对称轴x=1的对称点是点B(3,0)
∴由几何知识可知,PA+PC=PB+PC为最小.
在RT△BOC中,OC=3,OB=3;
∴BC=
| OC2+OB2 |
| 2 |
∴AP+CP的最小值为 3
| 2 |
点评:本题是二次函数的综合题型,主要涉及待定系数法求函数解析式,(2)中判断出点P的位置是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
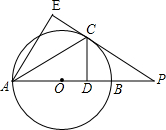 如图,⊙O中,AB是直径,AC是弦,CD⊥AB于D,将△ACD沿AC折叠得到△ACE,延长EC交AB的延长线于点P.
如图,⊙O中,AB是直径,AC是弦,CD⊥AB于D,将△ACD沿AC折叠得到△ACE,延长EC交AB的延长线于点P.