题目内容
45°和60°的两个三角板拼成四边形ABCD，求四边形ABCD各个角的度数，并猜想四边形四个内角的和是多少度．
考点：多边形内角与外角
专题：分类讨论
分析：根据题意作出图形后根据三角形的内角的度数确定四边形各个内角的度数即可．
解答：
解：如图，根据直角三角板的内角的度数知：
∠DAB=45°+30°=75°，
∠DCB=45°+60°=105°，
∠D=∠B=90°，
猜想：四边形的内角和为360°．
解：如图，根据直角三角板的内角的度数知：∠DAB=45°+30°=75°，
∠DCB=45°+60°=105°，
∠D=∠B=90°，
猜想：四边形的内角和为360°．
点评：本题考查了多边形的内角和外角，能够作出图形是解答本题的关键，难度不大．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
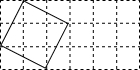如图，一个矩形由3×6的正方形网格组成，上有4条横线和7条竖线，称为网格的网线；这些网线之间有28个交叉点，称为网格的节点，以节点为顶点，边在网线上的正方形称为网线正方形；以节点为顶点，边不在网线上的正方形称为非网线正方形，图中已经画出了一个非网线正方形．那么，在图上能够画出的非网线正方形共有某一次函数的图象经过点（-1，2），且函数y的值随自变量x的增大而减小，则下列函数符合条件的是（ ）
| A、y=4x+6 |
| B、y=-x |
| C、y=-x+1 |
| D、y=-3x+5 |
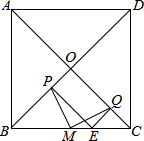如图所示，在正方形ABCD中，对角线AC，BD交于点O，M是BC的中点，E是BC上任意一点，EP⊥BD于点P，EQ⊥AC于点Q，连接MP和MQ，试说明MP=MQ．