题目内容
下列说法错误的有( )个
①无理数包括正无理数、零、负无理数;
②3.0×104精确到千位,有2个有效数字
③命题“若x2=1,则x=1”的逆命题是真命题;
④若等腰三角形一腰上的高等于腰长的一半,则此等腰三角形的底角为30°和60°;
⑤若两数和为-6,两数积为-1,则以这两数为根的一元二次方程的一次项系数为6.
①无理数包括正无理数、零、负无理数;
②3.0×104精确到千位,有2个有效数字
③命题“若x2=1,则x=1”的逆命题是真命题;
④若等腰三角形一腰上的高等于腰长的一半,则此等腰三角形的底角为30°和60°;
⑤若两数和为-6,两数积为-1,则以这两数为根的一元二次方程的一次项系数为6.
| A、1 | B、2 | C、3 | D、4 |
考点:根与系数的关系,近似数和有效数字,无理数,等腰三角形的性质,含30度角的直角三角形,命题与定理
专题:应用题
分析:①0是有理数,故0不是无理数;
②把3.0×104恢复原数,可观察3后第一个0的位置,a有几个有效数字,此近似数就有几个有效数字;
③先找出原命题的逆命题,再判断是否是真的;
④分两种情况讨论:再三角形内部和三角形外部,分别计算;
⑤根据根与系数的关系可知,此选项正确.
②把3.0×104恢复原数,可观察3后第一个0的位置,a有几个有效数字,此近似数就有几个有效数字;
③先找出原命题的逆命题,再判断是否是真的;
④分两种情况讨论:再三角形内部和三角形外部,分别计算;
⑤根据根与系数的关系可知,此选项正确.
解答: 解:①、0是有理数,故①选项错误;
解:①、0是有理数,故①选项错误;
②、3.0×104是精确到千位,且有两位有效数字,故②选项正确;
③命题“若x2=1,则x=1”的逆命题是“若x=1,则x2=1”,此逆命题是真命题,故③选项正确;
④分两种情况:
第一种情况,当高在三角形内部,在Rt△ABD中,由于BD=
AB,可知∠BAD=30°,
那么等腰三角形ABC的底角=75°;
第二种情况,当高在三角形的外部,在Rt△ABD中,由于BD=
AB,那么∠BAD=30°,
那么等腰三角形ABC的底角=15°.
故答案应该是15°或75°,此选项错误;
⑤若两数和为-6,两数积为-1,则以这两数为根的一元二次方程的一次项系数为6.
此选项错误.
故选C.
 解:①、0是有理数,故①选项错误;
解:①、0是有理数,故①选项错误;②、3.0×104是精确到千位,且有两位有效数字,故②选项正确;
③命题“若x2=1,则x=1”的逆命题是“若x=1,则x2=1”,此逆命题是真命题,故③选项正确;
④分两种情况:
第一种情况,当高在三角形内部,在Rt△ABD中,由于BD=
| 1 |
| 2 |
那么等腰三角形ABC的底角=75°;

第二种情况,当高在三角形的外部,在Rt△ABD中,由于BD=
| 1 |
| 2 |
那么等腰三角形ABC的底角=15°.
故答案应该是15°或75°,此选项错误;
⑤若两数和为-6,两数积为-1,则以这两数为根的一元二次方程的一次项系数为6.
此选项错误.
故选C.
点评:本题考查了近似数和有效数字、无理数、命题和逆命题、含有30°角的直角三角形的性质、根与系数的关系,解题的关键是熟练掌握有关概念,并能分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某区2009年应届初中毕业生为5.5万人,2010年、2011年两届毕业生一共为12.5万人,设2009年到2011年平均每年学生人数增长的百分率为x,则方程可列为( )
| A、5.5(1+x)2=12.5 |
| B、5.5+5.5(1+x)2=12.5 |
| C、5.5+5.5(1+x)+5.5(1+x)2=12.5 |
| D、5.5(1+x)+5.5(1+x)2=12.5 |
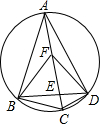 如图,四边形ABCD内接于⊙O,对角线AC与BD相交于点E、F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC,下列结论:
如图,四边形ABCD内接于⊙O,对角线AC与BD相交于点E、F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC,下列结论:①线段AC为⊙O的直径;②CD⊥DF;③BC=2CD;④∠AFB=∠BCD
其中正确的个数为( )
| A、0个 | B、1个 | C、2个 | D、3个 |
下列事件是必然事件的是( )
| A、通常加热到100°C时,水沸腾 |
| B、掷一次骰子,向上一面是6点 |
| C、度量三角形的内角和,结果是180° |
| D、某射击运动员射击一次,命中靶心 |

 如图是制作的一个圆锥形纸帽的示意图,围成这个纸帽的纸的面积为
如图是制作的一个圆锥形纸帽的示意图,围成这个纸帽的纸的面积为