题目内容
 如图,Rt△ABC的顶点A是直线AC(
如图,Rt△ABC的顶点A是直线AC( )与双曲线
)与双曲线 在第一象限的交点,C是直线
在第一象限的交点,C是直线 与x轴的交点,点B在x轴上,且∠ABC=90°,CB=AB,S△AOB=3.
与x轴的交点,点B在x轴上,且∠ABC=90°,CB=AB,S△AOB=3.
(1)求m的值;(2)求△ABC的面积.
解:(1)设A点坐标为(a,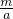 ),
),
则AB= ,OB=|a|,
,OB=|a|,
∴ ,
,
∴ ,
,
∴m=±6,
∵点A在第一象限,
∴m=6;
(2)∵C是直线 与x轴的交点,
与x轴的交点,
∴C点坐标为(-12,0),
∵CB=AB,点A在 上,
上,
∴A(-6+4 ,3+2
,3+2 )B(-6+4
)B(-6+4 ,0),
,0),
∴BC=6+4 ,AB=3+2
,AB=3+2 ,
,
∴S△ABC= ×(3+2
×(3+2 )×(6+4
)×(6+4 )=21+12
)=21+12 .
.
分析:(1)根据S△AOB=3,就可以得到函数的解析式,然后就得到m的值;
(2)由于C是直线 与x轴的交点,则C点坐标为(-12,0).这样就可以求出A,B的坐标,得到BC,然后就可以求出三角形的面积.
与x轴的交点,则C点坐标为(-12,0).这样就可以求出A,B的坐标,得到BC,然后就可以求出三角形的面积.
点评:本题考查函数图象交点坐标的求法及反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S= |k|.
|k|.
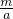 ),
),则AB=
 ,OB=|a|,
,OB=|a|,∴
 ,
,∴
 ,
,∴m=±6,
∵点A在第一象限,
∴m=6;
(2)∵C是直线
 与x轴的交点,
与x轴的交点,
∴C点坐标为(-12,0),
∵CB=AB,点A在
 上,
上,∴A(-6+4
 ,3+2
,3+2 )B(-6+4
)B(-6+4 ,0),
,0),∴BC=6+4
 ,AB=3+2
,AB=3+2 ,
,∴S△ABC=
 ×(3+2
×(3+2 )×(6+4
)×(6+4 )=21+12
)=21+12 .
.分析:(1)根据S△AOB=3,就可以得到函数的解析式,然后就得到m的值;
(2)由于C是直线
 与x轴的交点,则C点坐标为(-12,0).这样就可以求出A,B的坐标,得到BC,然后就可以求出三角形的面积.
与x轴的交点,则C点坐标为(-12,0).这样就可以求出A,B的坐标,得到BC,然后就可以求出三角形的面积.点评:本题考查函数图象交点坐标的求法及反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=
 |k|.
|k|. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线 如图,Rt△ABC的两直角边分别为1,2,以Rt△ABC的斜边AC为一直角边,另一直角边为1画第二个△ACD;在以△ACD的斜边AD为一直角边,另一直角边长为1画第三个△ADE;…,依此类推,第n个直角三角形的斜边长是
如图,Rt△ABC的两直角边分别为1,2,以Rt△ABC的斜边AC为一直角边,另一直角边为1画第二个△ACD;在以△ACD的斜边AD为一直角边,另一直角边长为1画第三个△ADE;…,依此类推,第n个直角三角形的斜边长是 如图,Rt△ABC的斜边AB=10cm,
如图,Rt△ABC的斜边AB=10cm,
 如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积.
如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积.