题目内容
如图，Rt△ABC的一条直角边AB是⊙O的直径，AB=8，斜边交⊙O于D，∠A=30°，求阴影部分的面积．分析：首先求出∠DOB=60°，再利用扇形面积公式求出S扇形DOB，再利用勾股定理求出AD的长，再利用三角形面积公式求出阴影部分面积即可．
解答：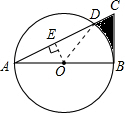
解：过点O作OE⊥AD于点E，连接DO，
∵∠A=30°，
∴∠DOB=60°，
∴S扇形DOB=
=
π，
∵∠A=30°，AO=4，∴EO=2，∴AE=2
，
∴AD=4
，
∵∠A=30°，AB=8，
∴BC=
×8=
，
∴S△ABC=
×8×
=
，
S△AOD=
×EO×AD=
×2×4
=4
，
∴阴影部分的面积为：
-4
-
π=
-
．
解：过点O作OE⊥AD于点E，连接DO，∵∠A=30°，
∴∠DOB=60°，
∴S扇形DOB=
| 60π×42 |
| 360 |
| 8 |
| 3 |
∵∠A=30°，AO=4，∴EO=2，∴AE=2
| 3 |
∴AD=4
| 3 |
∵∠A=30°，AB=8，
∴BC=
| ||
| 3 |
8
| ||
| 3 |
∴S△ABC=
| 1 |
| 2 |
8
| ||
| 3 |
32
| ||
| 3 |
S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴阴影部分的面积为：
32
| ||
| 3 |
| 3 |
| 8 |
| 3 |
20
| ||
| 3 |
| 8π |
| 3 |
点评：此题主要考查了扇形面积公式以及三角形面积公式和勾股定理得出应用，根据已知得出AD的长是解题关键．
练习册系列答案
相关题目
如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC边上的中线BD反向延长线交y轴负半轴于E，双曲线
如图，Rt△ABC的两直角边分别为1，2，以Rt△ABC的斜边AC为一直角边，另一直角边为1画第二个△ACD；在以△ACD的斜边AD为一直角边，另一直角边长为1画第三个△ADE；…，依此类推，第n个直角三角形的斜边长是
如图，Rt△ABC的斜边AB=10cm，