题目内容
A，B，C三家工厂，B，C的产量为a吨，A厂产量为2a吨，现需建一仓库D，AD等于x千米，BD等于y千米，CD等于z千米，每吨货物运行1千米需要费用10元，则总费w与x之间的关系式为 ，D选在何处时w最小？
考点：三角形三边关系
专题：
分析：利用路程×每千米的费用×重量可以表示出总费用w与x之间的关系，再利用三角形三边之间的关系分D在△ABC的内部（或外部）和D在A点两种情况分别讨论可得出结论．
解答：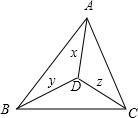
解：由题意可知：w=10×（2ax+ay+az）=10a（2x+y+z），
∵2x+y+z=x+y+x+z，
当D在△ABC内部（或外部）时，有x+y＞AB，x+z＞AC，
∴2x+y+x＞AB+AC，
当D与A重合时，x+y=AB，x+z=AC，
此时2x+y+x=AB+AC，
即当D和A重合时，2x+y+x的值最小，即w最小，所以D选在A点处，
故答案为：w=10a（2x+y+z）．
解：由题意可知：w=10×（2ax+ay+az）=10a（2x+y+z），∵2x+y+z=x+y+x+z，
当D在△ABC内部（或外部）时，有x+y＞AB，x+z＞AC，
∴2x+y+x＞AB+AC，
当D与A重合时，x+y=AB，x+z=AC，
此时2x+y+x=AB+AC，
即当D和A重合时，2x+y+x的值最小，即w最小，所以D选在A点处，
故答案为：w=10a（2x+y+z）．
点评：本题主要考查三角形的三边关系，解题的关键是把2x+y+z写成x+y+x+z再进行讨论．
练习册系列答案
相关题目
已知∠AOB=α，过点O任作一射线OC，OM平分∠AOC，ON平分∠BOC，
如图，C是线段AB上一点，△ACD和△BCE都是等边三角形，AE交CD于点M，BD交CE于点N，交AE于点O，求证：