题目内容
14.在平面直角坐标系中,有三点A(-1,0),B(0,$\sqrt{3}$),C(3,0).(1)求过点A、B、C的抛物线的解析式;
(2)如图1,在线段AC上有一动点P,过P点作直线PD∥AB交BC于点D,求出△PBD面积的最大值;
(3)如图2,在(2)的情况下,在抛物线上是否存在一点Q,使△QBD的面积与△PBD面积相等?如存在,直接写出Q点坐标;如不存在,请说明理由.

分析 (1)设交点式y=a(x+1)(x-3),然后把B点坐标代入求出a即可;
(2)先利用三角函数的定义计算出∠OAB=60°,∠OCB=30°,则∠ABC=90°,于是得到PD⊥BC,设P(m,0),则PC=3-m,接着表示出PD和BD,则根据三角形面积公式得到S△PBD=$\frac{1}{2}$PD•BD=-$\frac{\sqrt{3}}{8}$(m-1)2+$\frac{\sqrt{3}}{2}$,然后根据二次函数的性质求解;
(3)先利用待定系数法求出直线BC的解析式为y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,由于△QBD的面积与△PBD面积相等,则点P到BD的距离等于P点到BD的距离:当PQ∥BD时,可得到此时直线解析式为y=-$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$,于是通过解方程组$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}}\\{y=-\frac{\sqrt{3}}{3}{x}^{2}+\frac{2\sqrt{3}}{3}x+\sqrt{3}}\end{array}\right.$可得Q点坐标;当点P和Q在BD两侧,利用直线平行得到Q点为直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$与抛物线的交点,再通过解方程组$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+\frac{5\sqrt{3}}{3}}\\{y=-\frac{\sqrt{3}}{3}{x}^{2}+\frac{2\sqrt{3}}{3}x+\sqrt{3}}\end{array}\right.$得Q点坐标.
解答 解:(1)设抛物线解析式为y=a(x+1)(x-3),
把B(0,$\sqrt{3}$)代入得a•1•(-3)=$\sqrt{3}$,解得a=-$\frac{\sqrt{3}}{3}$,
所以抛物线解析式为y=-$\frac{\sqrt{3}}{3}$(x+1)(x-3),即y=-$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$;
(2)如图1,
∵OA=1,OB=$\sqrt{3}$,OC=3,
∴tan∠OAB=$\sqrt{3}$,tan∠OCB=$\frac{\sqrt{3}}{3}$,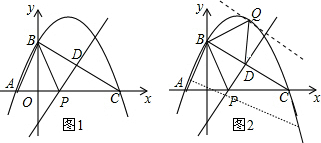
∴BC=2OB=2$\sqrt{3}$,
∴∠OAB=60°,∠OCB=30°,
∴∠ABC=90°,
∵PD∥AB,
∴PD⊥BC,
设P(m,0),则PC=3-m,
在Rt△PCD中,PD=$\frac{1}{2}$PC=$\frac{1}{2}$(3-m),CD=$\sqrt{3}$PD=$\frac{\sqrt{3}}{2}$(3-m),
∴BD=BC-CD=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$(3-m),
∴S△PBD=$\frac{1}{2}$PD•BD=$\frac{1}{2}$•$\frac{1}{2}$(3-m)•[2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$(3-m)]
=-$\frac{\sqrt{3}}{8}$(m-1)2+$\frac{\sqrt{3}}{2}$,
当m=1时,△PBD面积的最大值为$\frac{\sqrt{3}}{2}$;
(3)如图2,设直线BC的解析式为y=kx+b,
把B(0,$\sqrt{3}$),C(3,0)代入得$\left\{\begin{array}{l}{3k+b=0}\\{b=\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=\sqrt{3}}\end{array}\right.$,
∴直线BC的解析式为y=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,
过P点作BC的平行线交抛物线于Q,则△QBD的面积与△PBD面积相等,此时直线解析式为y=-$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$,
解方程组$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}}\\{y=-\frac{\sqrt{3}}{3}{x}^{2}+\frac{2\sqrt{3}}{3}x+\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{3+\sqrt{17}}{2}}\\{y=\frac{-\sqrt{3}-\sqrt{51}}{6}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{3-\sqrt{17}}{2}}\\{y=\frac{-\sqrt{3}+\sqrt{51}}{6}}\end{array}\right.$,此时Q点坐标为($\frac{3+\sqrt{17}}{2}$,$\frac{-\sqrt{3}-\sqrt{51}}{6}$)或($\frac{3-\sqrt{17}}{2}$,$\frac{-\sqrt{3}+\sqrt{51}}{6}$),
把直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$向上平移$\frac{4\sqrt{3}}{3}$个单位得到直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$,则直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{5\sqrt{3}}{3}$交抛物线于Q,则△QBD的面积与△PBD面积相等,
解方程组$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+\frac{5\sqrt{3}}{3}}\\{y=-\frac{\sqrt{3}}{3}{x}^{2}+\frac{2\sqrt{3}}{3}x+\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=\frac{4\sqrt{3}}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=\sqrt{3}}\end{array}\right.$,此时Q点坐标为(1,$\frac{4\sqrt{3}}{3}$)或(2,$\sqrt{3}$),
综上所述,Q点的坐标为($\frac{3+\sqrt{17}}{2}$,$\frac{-\sqrt{3}-\sqrt{51}}{6}$)或($\frac{3-\sqrt{17}}{2}$,$\frac{-\sqrt{3}+\sqrt{51}}{6}$)或(1,$\frac{4\sqrt{3}}{3}$)或(2,$\sqrt{3}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质和一次函数的平移变换;会利用待定系数法求函数解析式;记住含30度的直角三角形三边的关系;解决(3)小题的关键是把三角形面积相等的问题转化为到直线的距离相等.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案
| A. | 线段BE | B. | 线段EF | C. | 线段CE | D. | 线段DE |
| A. |  | B. |  | C. |  | D. |  |
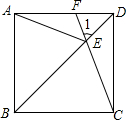 如图,在正方形ABCD中,E是对角线BD上任意一点(BE>DE),CE的延长线交AD于点F,连接AE.
如图,在正方形ABCD中,E是对角线BD上任意一点(BE>DE),CE的延长线交AD于点F,连接AE.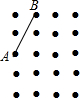 如图,在4×5的点阵图中,每两个横向和纵向相邻阵点的距离均为1,该点阵图中已有两个阵点分别标为A、B,请在此点阵图中找一个阵点C,使得以点A、B、C为顶点的三角形是等腰三角形,则符合条件的点C有5个.
如图,在4×5的点阵图中,每两个横向和纵向相邻阵点的距离均为1,该点阵图中已有两个阵点分别标为A、B,请在此点阵图中找一个阵点C,使得以点A、B、C为顶点的三角形是等腰三角形,则符合条件的点C有5个.
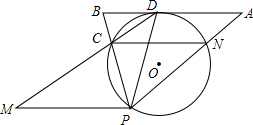 如图,在⊙O中,弧DC=弧DN,点P为⊙O上一点,过D作CN的平行线交PN,PC的延长线于A,B,过P作PM∥AB交DC的延长线于M.
如图,在⊙O中,弧DC=弧DN,点P为⊙O上一点,过D作CN的平行线交PN,PC的延长线于A,B,过P作PM∥AB交DC的延长线于M.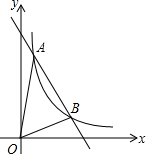 已知:反比例函数y1=$\frac{k}{x}$(k≠0,x>0)与一次函数y2=ax+b的图象相交于点A(1,8),B(4,m)两点.
已知:反比例函数y1=$\frac{k}{x}$(k≠0,x>0)与一次函数y2=ax+b的图象相交于点A(1,8),B(4,m)两点.