题目内容
17.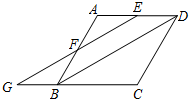 如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.
如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接EF并延长,交CB的延长线于点G,连接BD.(1)求证:四边形EGBD是平行四边形;
(2)连接AG,若∠FGB=30°,GB=AE=1,求AG的长.
分析 (1)连接AC,再根据菱形的性质得出EG∥BD,根据对边分别平行证明是平行四边形即可.
(2)过点A作AH⊥BC,再根据直角三角形的性质和勾股定理解答即可.
解答 (1)证明:连接AC,如图1: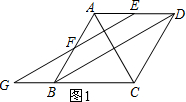
∵四边形ABCD是菱形,
∴AC平分∠DAB,且AC⊥BD,
∵AF=AE,
∴AC⊥EF,
∴EG∥BD.
又∵菱形ABCD中,ED∥BG,
∴四边形EGBD是平行四边形.
(2)解:过点A作AH⊥BC于H.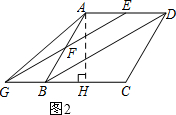
∵∠FGB=30°,
∴∠DBC=30°,
∴∠ABH=2∠DBC=60°,
∵GB=AE=1,
∴AB=AD=2,
在Rt△ABH中,∠AHB=90°,
∴AH=$\sqrt{3}$,BH=1.
∴GH=2,
在Rt△AGH中,
根据勾股定理得,AG=$\sqrt{7}$.
点评 本题考查了菱形性质,关键是根据菱形的性质和平行四边形的判定以及直角三角形的性质解题.

练习册系列答案
相关题目
8.某公司有5个股东,每个股东的利润相同,有100名工人,每名工人的工资相同.2015年第一个季度工人的工资总额与公司的股东总利润情况见表:
该公司老板根据表中数据,作出了图1,并声称股东利润和工人工资同步增长,公司和工人做到了“有福同享”.
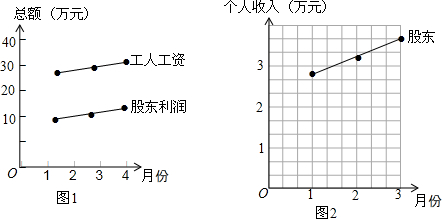
针对老板的说法,解决下列问题:
(1)这三个月工人个人的月收入分别是0.28,0.30,0.32万元;
(2)在图2中,已经做出这三个月每个股东利润统计图,请你补出这三个月工人个人月收入的统计图;
(3)通过完成第(1),(2)问和对图2的观察,你如何看待老板的说法?(用一两句话概括)
| 月份 | 工人工资总额(万元) | 股东总利润(万元) |
| 1 | 28 | 14 |
| 2 | 30 | 16 |
| 3 | 32 | 18 |

针对老板的说法,解决下列问题:
(1)这三个月工人个人的月收入分别是0.28,0.30,0.32万元;
(2)在图2中,已经做出这三个月每个股东利润统计图,请你补出这三个月工人个人月收入的统计图;
(3)通过完成第(1),(2)问和对图2的观察,你如何看待老板的说法?(用一两句话概括)
5.某超市货架上摆放着外观、颜色、样式、规格完全相同的盒装酸奶,其生产日期有三盒是“20150410”,五盒是“20150412”,两盒是“20150413”.若从中随机抽取一盒,恰好抽到生产日期为“20150413”的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
 如图,在梯形ABCD中,AD∥BC,若△AOB的面积为8cm2,那么△DOC的面积为多少?
如图,在梯形ABCD中,AD∥BC,若△AOB的面积为8cm2,那么△DOC的面积为多少?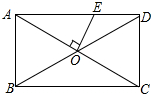 如图,矩形ABCD的对角线AC、BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值.
如图,矩形ABCD的对角线AC、BD相交于点O,过点O作OE⊥AC交AD于E,若AB=6,AD=8,求sin∠OEA的值.