题目内容
5. 如图,圆O通过五边形OABCD的四个顶点.若$\widehat{ABD}$=150°,∠A=65°,∠D=60°,则$\widehat{BC}$的度数为何?( )
如图,圆O通过五边形OABCD的四个顶点.若$\widehat{ABD}$=150°,∠A=65°,∠D=60°,则$\widehat{BC}$的度数为何?( )| A. | 25 | B. | 40 | C. | 50 | D. | 55 |
分析 连接OB,OC,由半径相等得到三角形OAB,三角形OBC,三角形OCD都为等腰三角形,根据∠A=65°,∠D=60°,求出∠1与∠2的度数,根据$\widehat{ABD}$的度数确定出∠AOD度数,进而求出∠3的度数,即可确定出$\widehat{BC}$的度数.
解答 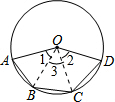 解:连接OB、OC,
解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=65°,∠D=60°,
∴∠1=180°-2∠A=180°-2×65°=50°,∠2=180°-2∠D=180°-2×60°=60°,
∵$\widehat{ABD}$=150°,
∴∠AOD=150°,
∴∠3=∠AOD-∠1-∠2=150°-50°-60°=40°,
则$\widehat{BC}$的度数为40°.
故选B
点评 此题考查了圆心角、弧、弦的关系,弄清圆心角、弧、弦的关系是解本题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
13.x=-3,y=1为下列哪一个二元一次方程式的解?( )
| A. | x+2y=-1 | B. | x-2y=1 | C. | 2x+3y=6 | D. | 2x-3y=-6 |
10. 如图,矩形ABCD中,M、E、F三点在$\overline{AD}$上,N是矩形两对角线的交点.若$\overline{AB}$=24,$\overline{AD}$=32,$\overline{MD}$=16,$\overline{ED}$=8,$\overline{FD}$=7,则下列哪一条直线是A、C两点的对称轴?( )
如图,矩形ABCD中,M、E、F三点在$\overline{AD}$上,N是矩形两对角线的交点.若$\overline{AB}$=24,$\overline{AD}$=32,$\overline{MD}$=16,$\overline{ED}$=8,$\overline{FD}$=7,则下列哪一条直线是A、C两点的对称轴?( )
 如图,矩形ABCD中,M、E、F三点在$\overline{AD}$上,N是矩形两对角线的交点.若$\overline{AB}$=24,$\overline{AD}$=32,$\overline{MD}$=16,$\overline{ED}$=8,$\overline{FD}$=7,则下列哪一条直线是A、C两点的对称轴?( )
如图,矩形ABCD中,M、E、F三点在$\overline{AD}$上,N是矩形两对角线的交点.若$\overline{AB}$=24,$\overline{AD}$=32,$\overline{MD}$=16,$\overline{ED}$=8,$\overline{FD}$=7,则下列哪一条直线是A、C两点的对称轴?( )| A. | 直线MN | B. | 直线EN | C. | 直线FN | D. | 直线DN |
17.若m=-2,则代数式m2-2m-1的值是( )
| A. | 9 | B. | 7 | C. | -1 | D. | -9 |
14. 如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
 如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )| A. | 16cm | B. | 18cm | C. | 20cm | D. | 21cm |
15.据统计,2015年“十•一”国庆长假期间,衢州市共接待国内外游客约319万人次,与2014年同比增长16.43%,数据319万用科学记数法表示为( )
| A. | 3.19×105 | B. | 3.19×106 | C. | 0.319×107 | D. | 319×106 |
 如图,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
如图,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)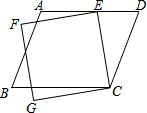 如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为何?( )
如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B的度数为何?( )