题目内容
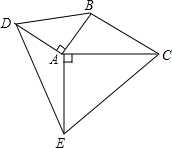 如图,在△ABC中,AB=2,BC=3,AC=4,△ABD和△ACE均为等腰直角三角形,则DE=
如图,在△ABC中,AB=2,BC=3,AC=4,△ABD和△ACE均为等腰直角三角形,则DE=考点:全等三角形的判定与性质
专题:
分析:先连接BE得到△ADC≌△ABE,进而得到∠DFB=90°从而得到四个直角三角形,在多次运用勾股定理可得出DE的长.
解答: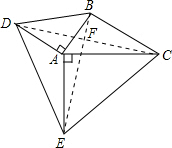 解:如图,连接BE、CD,BE与CD于F.
解:如图,连接BE、CD,BE与CD于F.
在△ADC与△ABE中,
,
∴△ADC≌△ABE(SDAS),
∴∠ADC=∠ABE.
∴∠DBF+∠BDF=90°
∴∠BFD=90°.
∴根据勾股定理得:DF2=BD2-BF2,EF2=CE2-CF2,BF2+CF2=BC2.
根据已知条件和勾股定理得BD=2
,CE=4
∴DE2=DF2+EF2
=BD2-BF2+CE2-CF2
=BD2+CE2-(BF2+CF2)
=BD2+CE2-BC2
=8+32-9
=31,
∴DE=
.
故答案是:
.
 解:如图,连接BE、CD,BE与CD于F.
解:如图,连接BE、CD,BE与CD于F.在△ADC与△ABE中,
|
∴△ADC≌△ABE(SDAS),
∴∠ADC=∠ABE.
∴∠DBF+∠BDF=90°
∴∠BFD=90°.
∴根据勾股定理得:DF2=BD2-BF2,EF2=CE2-CF2,BF2+CF2=BC2.
根据已知条件和勾股定理得BD=2
| 2 |
| 2 |
∴DE2=DF2+EF2
=BD2-BF2+CE2-CF2
=BD2+CE2-(BF2+CF2)
=BD2+CE2-BC2
=8+32-9
=31,
∴DE=
| 31 |
故答案是:
| 31 |
点评:本题考查了全等三角形的判定与性质.此题首先要巧妙构造辅助线发现全等三角形,进一步发现直角三角形,连续运用了勾股定理.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
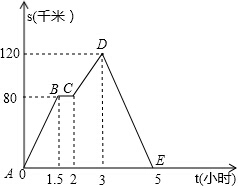 如图折线ABCDE描述了一汽车在某一直路上行驶时汽车离出发地的距离s(千米)和行驶时间t(小时)间的变量关系,则下列结论正确的是( )
如图折线ABCDE描述了一汽车在某一直路上行驶时汽车离出发地的距离s(千米)和行驶时间t(小时)间的变量关系,则下列结论正确的是( )| A、汽车共行驶了120千米 |
| B、汽车在行驶途中停留了2小时 |
| C、汽车在整个行驶过程中的平均速度为每小时24千米 |
| D、汽车自出发后3小时至5小时间行驶的速度为每小时60千米 |
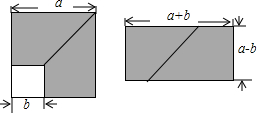 如图的分割正方形,拼接成长方形方案中,可以验证( )
如图的分割正方形,拼接成长方形方案中,可以验证( )| A、(a+b)2=a2+2ab+b2 |
| B、(a-b)2=a2-2ab+b2 |
| C、(a+b)2=(a+b)2-4ab |
| D、(a+b)(a-b)=a2-b2 |
 如图所示,在⊙O上取A、B两个点,测量出小于半圆的弧即
如图所示,在⊙O上取A、B两个点,测量出小于半圆的弧即
 如图,在△AFC中,B点为AC的中点,E为BD的中点,连接DE、AE,AE交CD于点F,则AF:AE=
如图,在△AFC中,B点为AC的中点,E为BD的中点,连接DE、AE,AE交CD于点F,则AF:AE=