题目内容
13.关于x的方程x2+x-a+1=0有实数根,则实数a的取值范围是a≥$\frac{3}{4}$.分析 根据方程x2+x-a+1=0有实数根得到根的判别式△≥0,列出a的不等式,求出a的取值范围.
解答 解:∵关于x的方程x2+x-a+1=0有实数根,
∴△=1-4(-a+1)≥0,
∴a≥$\frac{3}{4}$,
故答案为:a≥$\frac{3}{4}$.
点评 本题考查了根的判别式的知识,解答此题要掌握一元二次方程根的情况与判别式△的关系:
(1)△>0,方程有两个不相等的实数根;(2)△=0,方程有两个相等的实数根;
(3)△<0,方程没有实数根.反之也成立.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
1.下列事件:①在干燥的环境中,种子会发芽;②在排球比赛中弱队战胜强队;③抛掷10枚硬币,5枚正面向上;④彩票的中奖概率是8%,买100张有8张会中奖,其中随机事件有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8. 如图,点A、B、C都在⊙O上,点B为弧AC的中点,若∠AOB=72°,则∠OAC的度数是( )
如图,点A、B、C都在⊙O上,点B为弧AC的中点,若∠AOB=72°,则∠OAC的度数是( )
 如图,点A、B、C都在⊙O上,点B为弧AC的中点,若∠AOB=72°,则∠OAC的度数是( )
如图,点A、B、C都在⊙O上,点B为弧AC的中点,若∠AOB=72°,则∠OAC的度数是( )| A. | 18° | B. | 30° | C. | 36° | D. | 72° |
2.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{1.2}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
3.计算tan60°的值等于( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
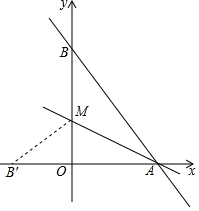 如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和点B,M是OB上的一点若将△ABM沿直线AM折叠,点B恰好落在x轴上的点B’处.
如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和点B,M是OB上的一点若将△ABM沿直线AM折叠,点B恰好落在x轴上的点B’处.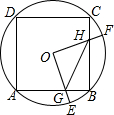 如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A,B重合),点F是$\widehat{BC}$上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
如图,边长为4的正方形ABCD内接于点O,点E是$\widehat{AB}$上的一动点(不与A,B重合),点F是$\widehat{BC}$上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:


