题目内容
如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时点P的坐标;
(3)在对称轴l上是否存在一点Q,使∠DQO=∠DCO?若存在,求出Q点坐标;若不存在,请说明理由.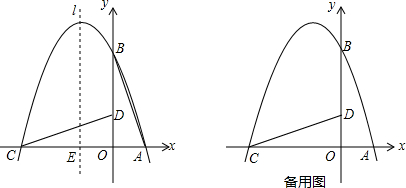
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时点P的坐标;
(3)在对称轴l上是否存在一点Q,使∠DQO=∠DCO?若存在,求出Q点坐标;若不存在,请说明理由.

考点:二次函数综合题
专题:
分析:(1)由条件可求得A、B、C三点的坐标分别为(1,0)、(0,3)、C(-3,0),代入解析式可求得抛物线的解析式;
(2)若△CEF与△COD相似,则有∠CFE=90°或∠CEF=90°,当∠CFE=90°时,连接PE并延长交y轴于点H,根据题意可证明△ODC≌△OEH,则OH=OC,可求得Q的坐标,结合E点坐标,可求出直线PH的解析式,联立直线和抛物线的解析式可求得P点坐标;当∠CEF=90°时,可知P点为抛物线的顶点;
(3)以CD为直径作圆,则该圆与对称轴l的交点即为所求的Q点,由勾股定理可求得CD的长,设CD中点为G,过G作GM⊥l于点M,作GN⊥x轴于点N,则可求出GQ的长,进一步可得出Q点的坐标.
(2)若△CEF与△COD相似,则有∠CFE=90°或∠CEF=90°,当∠CFE=90°时,连接PE并延长交y轴于点H,根据题意可证明△ODC≌△OEH,则OH=OC,可求得Q的坐标,结合E点坐标,可求出直线PH的解析式,联立直线和抛物线的解析式可求得P点坐标;当∠CEF=90°时,可知P点为抛物线的顶点;
(3)以CD为直径作圆,则该圆与对称轴l的交点即为所求的Q点,由勾股定理可求得CD的长,设CD中点为G,过G作GM⊥l于点M,作GN⊥x轴于点N,则可求出GQ的长,进一步可得出Q点的坐标.
解答:解:(1)∵tan∠BAO=
,
∴
=3,解得BO=3,
又由旋转可得OC=OB=3,
∴A、B、C三点的坐标分别为(1,0)、(0,3)、C(-3,0),
代入二次函数解析式可得
,
解得
.
∴抛物线的解析式为:y=-x2-2x+3;
(2)∵∠DOC=90°,
∴当△CEF与△COD相似,有∠CFE=90°或∠CEF=90°,
当∠CFE=90°时,连接PE并延长交y轴于点H,如图1,

由题意可知l方程为x=-1,∴OD=OE,
∵∠DCO+∠CDO=∠CDO+∠EHO=90°,
∴∠DCO=∠EHO,
在△ODC和△OEH中,
,
∴△ODC≌△OEH(AAS),
∴OH=OC=3,
∴H坐标为(0,-3),且E(-1,0),
设直线PH解析式为y=kx-3,把E点坐标代入可得-k-3=0,解得k=-3,
∴直线PH解析式为y=-3x-3,
联立抛物线线解析式可得
,解得
或
,
∵P点在第二象限,
∴P点坐标为(-2,3);
当∠CEF=90°时,则PE∥y轴,故P点坐标为抛物线的顶点,可求得P点坐标为(-1,4);
综上可知当△CEF与△COD相似时点P的坐标为(-2,3)或(-1,4);
(3)如图2,以CD为直径作圆,设其圆心为G,交对称于点Q、Q′,过G分别作GM⊥l,GN⊥x轴,垂足分别为M、N,连接GQ,

由圆周角定理可知∠DQO=∠DQ′O=DCO,
在Rt△CDO中,由勾股定理可得CD=
,则GQ=
CD=
,
又∵G为CD中点,则N为CO中点,可得ON=
OC=
,且OE=1,GN=
OD=
,
∴GM=NE=ON-OE=
-1=
,ME=GN=
,
在Rt△GMQ中,由勾股定理可得QM=
=
=
,
由垂径定理可得Q′M=QM=
,
∴QE=QM+ME=
+
=2,Q′E=Q′M-ME=
-
=1,且OE=1,
∴在对称轴l上是存在一点Q,使∠DQO=∠DCO,其坐标为(-1,2)或(-1,1).
| BO |
| AO |
∴
| BO |
| 1 |
又由旋转可得OC=OB=3,
∴A、B、C三点的坐标分别为(1,0)、(0,3)、C(-3,0),
代入二次函数解析式可得
|
解得
|
∴抛物线的解析式为:y=-x2-2x+3;
(2)∵∠DOC=90°,
∴当△CEF与△COD相似,有∠CFE=90°或∠CEF=90°,
当∠CFE=90°时,连接PE并延长交y轴于点H,如图1,

由题意可知l方程为x=-1,∴OD=OE,
∵∠DCO+∠CDO=∠CDO+∠EHO=90°,
∴∠DCO=∠EHO,
在△ODC和△OEH中,
|
∴△ODC≌△OEH(AAS),
∴OH=OC=3,
∴H坐标为(0,-3),且E(-1,0),
设直线PH解析式为y=kx-3,把E点坐标代入可得-k-3=0,解得k=-3,
∴直线PH解析式为y=-3x-3,
联立抛物线线解析式可得
|
|
|
∵P点在第二象限,
∴P点坐标为(-2,3);
当∠CEF=90°时,则PE∥y轴,故P点坐标为抛物线的顶点,可求得P点坐标为(-1,4);
综上可知当△CEF与△COD相似时点P的坐标为(-2,3)或(-1,4);
(3)如图2,以CD为直径作圆,设其圆心为G,交对称于点Q、Q′,过G分别作GM⊥l,GN⊥x轴,垂足分别为M、N,连接GQ,

由圆周角定理可知∠DQO=∠DQ′O=DCO,
在Rt△CDO中,由勾股定理可得CD=
| 10 |
| 1 |
| 2 |
| ||
| 2 |
又∵G为CD中点,则N为CO中点,可得ON=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴GM=NE=ON-OE=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△GMQ中,由勾股定理可得QM=
| GQ2-GM2 |
(
|
| 3 |
| 2 |
由垂径定理可得Q′M=QM=
| 3 |
| 2 |
∴QE=QM+ME=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴在对称轴l上是存在一点Q,使∠DQO=∠DCO,其坐标为(-1,2)或(-1,1).
点评:本题主要考查二次函数解析式和相似三角形的判定和性质、圆周角定理、勾股定理等知识的综合应用.在(1)中注意待定系数法是求函数解析式的常用方法,关键是求得点的坐标;在(2)中利用相似求得直线PE于y轴的交点坐标是解题的关键,注意方程思想的应用;在(3)中利用圆周角定理确定出Q点的位置是解题的关键,注意垂径定理的应用.本题知识点考查较多,综合性较强,难度较大.

练习册系列答案
相关题目