题目内容
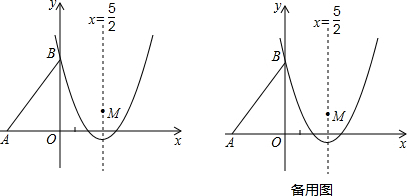
设A和B为抛物线y=-3x2-2x+k与x轴的两个相异交点,M为抛物线的顶点,若△ABM为Rt△,求k的值.分析:先由根的判别式求出k的取值范围,再画出图形,利用抛物线的顶点式表示出M的坐标,利用抛物线的对称性及等腰三角形的性质可知MN=
AB,由两点间的距离公式即可用k表示出AB的值,再由MN=
AB即可求出k的值.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:如图,因抛物线与x轴有两个相异的交点,
解:如图,因抛物线与x轴有两个相异的交点,
所以△=4-4k×(-3)>0,
解得,k>-
,依题意∠AMB=90°,AM=BM,过M作MN⊥x轴于N,则显然有MN=
AB,
又因MN=
=k+
,
AB=
,
=
,
=
,
=
,
所以k+
=
×
.
解得k1=0,k2=-
(舍去).
故答案为:k=0.
 解:如图,因抛物线与x轴有两个相异的交点,
解:如图,因抛物线与x轴有两个相异的交点,所以△=4-4k×(-3)>0,
解得,k>-
| 1 |
| 3 |
| 1 |
| 2 |
又因MN=
| 4k×(-3)-4 |
| 4×(-3) |
| 1 |
| 3 |
AB=
| (x1-x2)2 |
=
| (x1+x2)2-4x1x2 |
=
(-
|
=
| 2 |
| 3 |
| 1+3k |
所以k+
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1+3k |
解得k1=0,k2=-
| 1 |
| 3 |
故答案为:k=0.
点评:本题考查的是二次函数的图象与x轴的交点问题,熟知二次函数的性质、等腰三角形的性质及两点间的距离公式是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 大值,并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
大值,并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;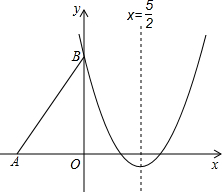 (2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
(2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=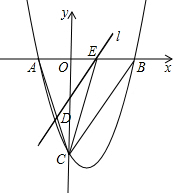 (2012•东莞)如图,抛物线y=
(2012•东莞)如图,抛物线y=