��Ŀ����
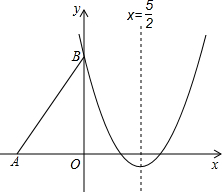 ��2012•���ݣ���ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=
��2012•���ݣ���ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=| 2 |
| 3 |
| 5 |
| 2 |
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2�����ѡ�ABO��x������ƽ�Ƶõ���DCE����A��B��O�Ķ�Ӧ��ֱ���D��C��E�����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ��ڸ��������ϣ���˵�����ɣ�
��3���ڣ�2���������£�����BD����֪�Գ����ϴ���һ��Pʹ�á�PBD���ܳ���С�����P������ꣻ
��4���ڣ�2������3���������£�����M���߶�OB�ϵ�һ�����㣨��M���O��B���غϣ�������M����BD��x���ڵ�N������PM��PN����OM�ij�Ϊt����PMN�����ΪS����S��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��S�Ƿ�������ֵ�������ڣ�������ֵ�ʹ�ʱM������ꣻ�������ڣ�˵�����ɣ�
��������1������������y=
x2+bx+c������B��0��4�����Լ�������ֱ��x=
�ϣ��ó�b��c���ɣ�
��2���������ε����ʵó�C��D���������ֱ��ǣ�5��4������2��0��������ͼ���ϵ�����ʵó�x=5��2ʱ��y��ֵ���ɣ�
��3��������ֱ��CD��Ӧ�ĺ�����ϵʽΪy=kx+b���������ʽ����x=
ʱ�����y���ɣ�
��4������MN��BD���ó���OMN�ס�OBD�������ó�
=
���õ�ON=
t��������ʾ����PMN����������ö��κ�����ֵ������ɣ�
| 2 |
| 3 |
| 5 |
| 2 |
��2���������ε����ʵó�C��D���������ֱ��ǣ�5��4������2��0��������ͼ���ϵ�����ʵó�x=5��2ʱ��y��ֵ���ɣ�
��3��������ֱ��CD��Ӧ�ĺ�����ϵʽΪy=kx+b���������ʽ����x=
| 5 |
| 2 |
��4������MN��BD���ó���OMN�ס�OBD�������ó�
| OM |
| OB |
| ON |
| OD |
| 1 |
| 2 |
����⣺��1����������y=
x2+bx+c������B��0��4��
��c=4��
�߶�����ֱ��x=
�ϣ�
��-
=-
=
��
��b=-
��
����������ϵʽΪy=
x2-
x+4��
��2����Rt��ABO��OA=3��OB=4��
��AB=
=5��
���ı���ABCD�����Σ�
��BC=CD=DA=AB=5��
��C��D���������ֱ��ǣ�5��4������2��0����
��x=5ʱ��y=
��52-
��5+ 4=4��
��x=2ʱ��y=
��22-
��2+ 4=0��
���C�͵�D���������������ϣ�
��3����CD��Գ��ύ�ڵ�P����PΪ����ĵ㣬
��ֱ��CD��Ӧ�ĺ�����ϵʽΪy=kx+b��
��
��
��ã�
��
��y=
x-
��
��x=
ʱ��y=
��
-
=
��
��P��
��
����
��4����MN��BD��
���OMN�ס�OBD��
��
=
��
=
��ON=
t��
��Գ��ύx�ڵ�F��
��S����PFOM=
��PF+OM��•OF=
��
+t����
=
t+
��
��S��MON=
OM•ON=
t•
t=
t2��
S��PNF=
��NF•PF=
����
-
t����
=-
t+
��
S=
t+
-
t2 -��-
t+
����
=-
t2+
t��0��t��4����
a=-
��0�������߿������£�S�������ֵ��
��S��PMN=-
t2+
t=-
��t-
��2+
��
�൱t=
ʱ��Sȡ���ֵ��
��
��ʱ����M������Ϊ��0��
����
| 2 |
| 3 |
��c=4��
�߶�����ֱ��x=
| 5 |
| 2 |
��-
| b |
| 2a |
| b | ||
2��
|
| 5 |
| 2 |
��b=-
| 10 |
| 3 |
����������ϵʽΪy=
| 2 |
| 3 |
| 10 |
| 3 |
��2����Rt��ABO��OA=3��OB=4��
��AB=
| OA2+OB2 |
���ı���ABCD�����Σ�
��BC=CD=DA=AB=5��
��C��D���������ֱ��ǣ�5��4������2��0����
��x=5ʱ��y=
| 2 |
| 3 |
| 10 |
| 3 |
��x=2ʱ��y=
| 2 |
| 3 |
| 10 |
| 3 |
���C�͵�D���������������ϣ�
��3����CD��Գ��ύ�ڵ�P����PΪ����ĵ㣬
��ֱ��CD��Ӧ�ĺ�����ϵʽΪy=kx+b��
��
|
��ã�
|
��y=
| 4 |
| 3 |
| 8 |
| 3 |
��x=
| 5 |
| 2 |
| 4 |
| 3 |
| 5 |
| 2 |
| 8 |
| 3 |
| 2 |
| 3 |
��P��
| 5 |
| 2 |
| 2 |
| 3 |
��4����MN��BD��
���OMN�ס�OBD��
��
| OM |
| OB |
| ON |
| OD |
| t |
| 4 |
| ON |
| 2 |
| 1 |
| 2 |
��Գ��ύx�ڵ�F��
��S����PFOM=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 6 |

��S��MON=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
S��PNF=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
S=
| 5 |
| 4 |
| 5 |
| 6 |
| 1 |
| 4 |
| 1 |
| 6 |
| 5 |
| 6 |
=-
| 1 |
| 4 |
| 17 |
| 12 |
a=-
| 1 |
| 4 |
��S��PMN=-
| 1 |
| 4 |
| 17 |
| 12 |
| 1 |
| 4 |
| 17 |
| 6 |
| 289 |
| 144 |
�൱t=
| 17 |
| 6 |
| 289 |
| 144 |
��ʱ����M������Ϊ��0��
| 17 |
| 6 |
������������Ҫ�����˶��κ������ۺ�Ӧ�ã��Լ��������ʺʹ���ϵ���������ʽ����ͼ�������ֵ�����ö��κ�������ֵ����ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
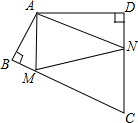 ��2012•���ݣ���ͼ���ı���ABCD�У���BAD=120�㣬��B=��D=90�㣬��BC��CD�Ϸֱ���һ��M��N��ʹ��AMN�ܳ���Сʱ�����AMN+��ANM�Ķ���Ϊ��������
��2012•���ݣ���ͼ���ı���ABCD�У���BAD=120�㣬��B=��D=90�㣬��BC��CD�Ϸֱ���һ��M��N��ʹ��AMN�ܳ���Сʱ�����AMN+��ANM�Ķ���Ϊ�������� ��2012•���ݣ���ͼ������ͬ��Բ����Բ�뾶Ϊ5cm��СԲ�İ뾶Ϊ3cm������Բ����AB��СԲ�ཻ������AB��ȡֵ��Χ��
��2012•���ݣ���ͼ������ͬ��Բ����Բ�뾶Ϊ5cm��СԲ�İ뾶Ϊ3cm������Բ����AB��СԲ�ཻ������AB��ȡֵ��Χ�� ��2012•���ݣ���ͼ��MΪ˫����y=
��2012•���ݣ���ͼ��MΪ˫����y=