题目内容
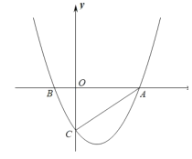
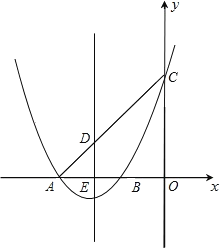
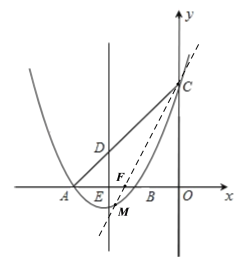
【题目】如图,已知抛物线![]() 交x轴于A.B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(1,0).
交x轴于A.B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(1,0).
(1)求抛物线的对称轴及点A的坐标;
(2)连结CA与抛物线的对称轴交于点D.
①在对称轴上找一点P,使ΔAPC为直角三角形,求点P的坐标.
②在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
【答案】(1)抛物线的对称轴为![]() ;点A的坐标为
;点A的坐标为![]() ;(2)①点P坐标为
;(2)①点P坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;②存在这样的点
;②存在这样的点![]() ,此时直线CM的解析式为
,此时直线CM的解析式为![]() .
.
【解析】
(1)令![]() 解关于x的一元二次方程可得点A坐标;再将抛物线的解析式化为顶点式可得对称轴;
解关于x的一元二次方程可得点A坐标;再将抛物线的解析式化为顶点式可得对称轴;
(2)①先求出点C坐标,再根据直角三角形的定义分三种情况,然后分别根据勾股定理求解即可得;
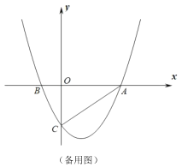
②如图(见解析),先求出四边形DEOC的面积,从而可得![]() 的面积,再根据三角形的面积公式可得OF的长,从而可得点F坐标,然后利用待定系数法可求出直线CM的解析式,最后联立一次函数和二次函数的解析式,看是否有交点即可得.
的面积,再根据三角形的面积公式可得OF的长,从而可得点F坐标,然后利用待定系数法可求出直线CM的解析式,最后联立一次函数和二次函数的解析式,看是否有交点即可得.
(1)令![]() 得
得![]()
解得![]() 或
或![]()
则点A的坐标为![]()
二次函数![]() 化为顶点式
化为顶点式![]()
则抛物线的对称轴为![]() ;
;
(2)①令![]() 得
得![]() ,则点C坐标为
,则点C坐标为![]()
设点P坐标为![]()
![]()
![]()
![]()
由直角三角形的定义,分以下三种情况:
当PA为斜边时,则![]()
即![]() ,解得
,解得![]()
此时,点P坐标为![]()
当PC为斜边时,则![]()
即![]() ,解得
,解得![]()
此时,点P坐标为![]()
当AC为斜边时,则![]()
即![]() ,解得
,解得![]()
此时,点P坐标为![]() 或
或![]()
综上,点P坐标为![]() 或
或![]() 或
或![]() 或
或![]() ;
;
②存在,求解过程如下:
∵![]() 轴,
轴,![]()
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四边形DEOC为直角梯形
,四边形DEOC为直角梯形
![]() 是等腰直角三角形
是等腰直角三角形
![]()
![]()
设直线CM的解析式为![]() ,与OE的交点为点F
,与OE的交点为点F
由题意得:![]()
解得![]()
![]()
将点![]() 代入直线CM的解析式得:
代入直线CM的解析式得: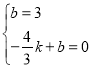
解得![]()
则直线CM的解析式为![]()
联立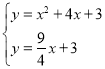 ,解得
,解得![]() 或
或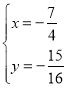
故存在这样的点![]() ,此时直线CM的解析式为
,此时直线CM的解析式为![]() .
.

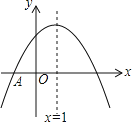
【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.