题目内容
16.已知关于x的方程x2-2x+m=0有两个不相等的实数根x1,x2.(1)求m的取值范围;
(2)若x1+x2-x1x2=6,求m的值.
分析 (1)由方程有两个不相等的实数根结合根的判别式,即可得出△=4-4m>0,解之即可得出m的取值范围;
(2)根据根与系数的关系可得出x1+x2=2、x1x2=m,结合x1+x2-x1x2=6可得出关于m的一元一次方程,解之即可得出结论.
解答 解:(1)∵关于x的方程x2-2x+m=0有两个不相等的实数根x1,x2,
∴△=(-2)2-4m=4-4m>0,
解得:m<1.
(2)∵方程x2-2x+m=0的两根为x1,x2,
∴x1+x2=2,x1x2=m.
∵x1+x2-x1x2=6,
∴2-m=6,
∴m=-4.
点评 本题考查了根的判别式以及根与系数的关系,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根”;(2)根据根与系数的关系结合x1+x2-x1x2=6,找出关于m的一元一次方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.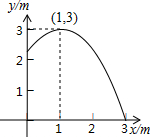 如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
 如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )
如图,池中心竖直水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管的长为( )| A. | 2.1m | B. | 2.2m | C. | 2.3m | D. | 2.25m |
1. 已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是( )
已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是( )
 已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是( )
已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是( )| A. | m>0 | B. | n<0 | C. | mn>0 | D. | m-n<0 |
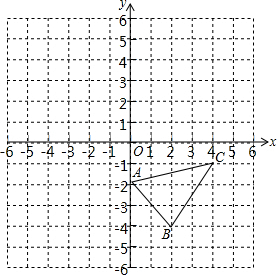 如图,平面直角坐标系中△ABC,分别画出与△ABC关于x轴、y轴对称的△A1B1C1和△A2B2C2,并写出△A1B1C1和△A2B2C2各顶点坐标.
如图,平面直角坐标系中△ABC,分别画出与△ABC关于x轴、y轴对称的△A1B1C1和△A2B2C2,并写出△A1B1C1和△A2B2C2各顶点坐标.