题目内容
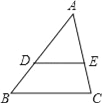
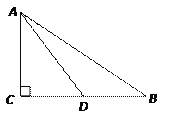
【题目】如图,在![]() 中,
中,![]() ,点D是BC边上的一点,
,点D是BC边上的一点,![]() ,
,![]() ,
,![]() .
.
(1)求AC和AB的长;
(2)求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题(1)在Rt△ACD中,利用![]() ,CD=6求出AD的长,再求出AC的长.再在Rt△ABC中,利用
,CD=6求出AD的长,再求出AC的长.再在Rt△ABC中,利用![]() =
=![]() =
=![]() 求出BC的长,再求出AB的长;(2)过点D作DH⊥AB于点H,利用S△ABD=
求出BC的长,再求出AB的长;(2)过点D作DH⊥AB于点H,利用S△ABD=![]() AB·DH=
AB·DH=![]() BD·AC,其中AB、BD、AC都可知,则可求出DH,再在Rt△ADH中利用正弦三角形函数定义求解.
BD·AC,其中AB、BD、AC都可知,则可求出DH,再在Rt△ADH中利用正弦三角形函数定义求解.
解:(1)∵在Rt△ACD中,cos∠ADC=![]() =
=![]() ,CD=6,
,CD=6,
∴AD=10,
∴在Rt△ACD中,AC=![]() =8.
=8.
又∵在Rt△ABC中,![]() =
=![]() =
=![]() ,
,
∴BC=12,
∴AB=![]() =4
=4![]() .
.
(2)过点D作DH⊥AB于点H,
∴S△ABD=![]() AB·DH=
AB·DH=![]() BD·AC,
BD·AC,
其中AB=4![]() ,BD=BC-CD=6,AC=8,
,BD=BC-CD=6,AC=8,
∴DH=![]() =
=![]() ,
,
∴在Rt△ADH中,sin∠BAD=![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目