题目内容
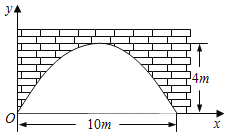
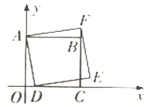
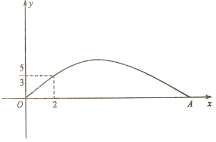
【题目】在某场足球比赛中，球员甲在球门正前方点O处起脚射门，在不受阻挡的情况下，足球沿如图所示的抛物线飞向球门中心线，当足球飞行的水平距离为2 m时，高度为
，落地点A距O点12 m．已知点O距球门9 m，球门的横梁高为2.44 m．
（1）飞行的足球能否射入球门？通过计算说明理由；
（2）若守门员乙站在球门正前方2 m处，他跳起时能摸到的最大高度为2.52 m，他能阻止此次射门吗？并写明理由．
【答案】（1）能射入球门．理由见解析；（2）不能阻止．理由见解析.
【解析】
（1）设抛物线解析式为
，将
代入求解析式，再将
代入即可判断；
（2）根据“守门员乙站在球门正前方2m处”可知此时x=7，将其代入解析式即可判断.
解：（1）能射入球门.
设抛物线解析式为
将代入求解可得：
抛物线解析式为
当时，
-
∵
，
∴能射入球门．
（2）不能阻止．
∵守门员乙站在球门正前方2 m处，
∴
当时，
∵
，
∴不能阻止．
怎样学好牛津英语系列答案
【题目】近一周，各个学校均在紧张有序的进行中考模拟考试，学生们通过模拟考试来调整自己的状态并了解自己的学业水平．某中学物理教研组想通过此次中考模拟的成绩来预估中考的各个分数段人数，在全年级随机抽取了男、女各40名学生的成绩，并将数据进行整理分析，给出了下面部分信息：
①男生成绩扇形统计图和女生成绩频数分布直方图如下：（数据分组为A组：x＜50，B组：50≤x＜60，C组：60≤x＜70，D组：70≤x≤80）
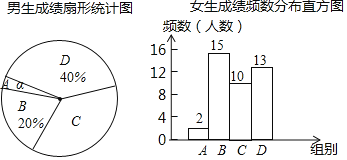
②男生C组中全部15名学生的成绩为：63，69，64，62，68，69，65，69，65，66，67，61，67，66，69
③两组数据的平均数、中位数、众数、满分率、极差（单位：分）如表所示：
平均数 | 中位数 | 众数 | 满分率 | 极差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
（1）扇形统计图A组学生对应的圆心角α的度数为______．
（2）若成绩在70分（包含70分）以上为优秀，请你估计该校1200名学生此次考试中优秀的人数．
