Question

【题目】如图，⊙O的直径CD，AB是⊙O的弦，AB⊥CD，垂足为N．连接AC．

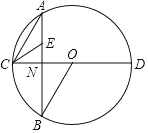
(1)若ON＝1，BN=．求弧BC长度；

(2)若点E在AB上，且AC2＝AE.AB．求证：∠CEB＝2∠CAB．

Answer 1

【答案】（1） ；（2）见解析

【解析】

(1)解Rt△OBN，得出OB= =2，tan∠BON==，那么∠BON＝60°，再利用弧长公式即可求出的长度；
(2)连接BC．根据垂径定理的推论得出=，那么∠1＝∠A．再证明△ACE∽△ABC，得出∠2＝∠1，等量代换得到∠A＝∠2，利用三角形外角的性质得出∠CEB＝∠A+∠2＝2∠A．

(1)∵AB⊥CD，垂足为N，
∴∠BNO＝90°．
在Rt△OBN中，∵ON＝1，BN=，
∴OB= =2，tan∠BON==，
∴∠BON＝60°，
∴的长度为：=；
(2)证明：如图，连接BC．
∵⊙O的直径是CD，AB⊥CD，
∴=，
∴∠1＝∠A．
∵AC2＝AEAB，
∴=，

又∠A＝∠A，
∴△ACE∽△ABC，
∴∠2＝∠1，
∴∠A＝∠2，
∴∠CEB＝∠A+∠2＝2∠A，
即∠CEB＝2∠CAB．