题目内容
14．
如图，正八边形的每个外角的度数是45°．
分析 根据正多边形的外角和是360°，每个外角都相等，则用360°除以边数即可求得外角的度数，然后根据内角和外角互为邻补角求得内角的度数．
解答 解：360°÷8=45°，
故答案为：45°．
点评 本题考查正多边形的计算，理解正多边形的外角和以及每个外角都相等是关键．
练习册系列答案
相关题目
4．下列说法正确的有（ ）
| A． | a一定是正数 | B． | $\frac{7}{3}$是有理数 | ||
| C． | 0.5不是有理数 | D． | 平方等于自身的数只有1个 |
如图，△ABC与△ADE关于直线MN对称，BC与DE的交点F在直线MN上．
2．-3的相反数是（ ）
| A． | -3 | B． | -$\frac{1}{3}$ | C． | 3 | D． | $\frac{1}{3}$ |
9．若一个三角形的两边长分别是3和6，则第三边的长可能是（ ）
| A． | 10 | B． | 2 | C． | 3 | D． | 4 |
如图，∠1=∠2，AC=AD，AB=AE，求证：△ABC≌△AED．
6．
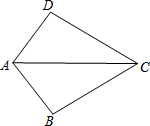如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）| A． | CB=CD | B． | ∠BAC=∠DAC | C． | ∠BCA=∠DAC | D． | ∠B=∠D=90° |
4．计算：（$\frac{-5{x}^{2}y}{3x}$）2的结果是（ ）
| A． | $\frac{10{x}^{4}y}{6x}$ | B． | $\frac{25{x}^{4}y}{9x}$ | C． | $\frac{25{x}^{4}{y}^{2}}{9{x}^{2}}$ | D． | $\frac{-5{x}^{4}{y}^{2}}{3{x}^{2}}$ |