题目内容
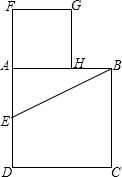如图，设AB是已知线段，在AB上作正方形ABCD；取AD的中点E，连接EB；延长DA至F，使EF=EB；以线段AF为边作正方形AFGH．则点H是AB的黄金分割点．为什么说上述的方法作出的点H是这条线段的黄金分割点，你能说出其中的道理吗？请试一试，说一说．
分析：根据黄金分割点的定义，只需证明AH2=AB•HB即可．
解答：解：设正方形ABCD的边长为2，
在Rt△AEB中，依题意，得AE=1，AB=2，
由勾股定理知EB=
=
=
，
∴AH=AF=EF-AE=EB-AE=
-1，
HB=AB-AH=3-
；
∴AH2=（
-1）2=6-2
，
AB•HB=2×（3-
）=6-2
，
∴AH2=AB•HB，
所以点H是线段AB的黄金分割点．
在Rt△AEB中，依题意，得AE=1，AB=2，
由勾股定理知EB=
| AB2+AE2 |
| 4+1 |
| 5 |
∴AH=AF=EF-AE=EB-AE=
| 5 |
HB=AB-AH=3-
| 5 |
∴AH2=（
| 5 |
| 5 |
AB•HB=2×（3-
| 5 |
| 5 |
∴AH2=AB•HB，
所以点H是线段AB的黄金分割点．
点评：能够根据已知条件结合勾股定理求得线段的长，能够用黄金分割点的定义进行证明．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
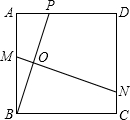垂直平分线，与AB、BP、CD分别交于点M、O、N，设AP=x．
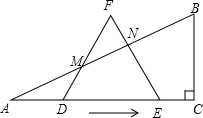），使边DF、EF与边AB分别相交于点M、N（M、N不与A、B重合）．
如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．
的一个动点(点C不与A、B重合)．
交于点P，试猜想点P在
上的位置是否会随点C的运动而变化?请说明理由．
