题目内容
 如图,点B是函数y=
如图,点B是函数y= 和y=x的图象在第一象限的交点,点E在函数y=
和y=x的图象在第一象限的交点,点E在函数y= 的图象上,过B、E两点作x轴的垂线,垂足分别为C、F,直线EF与直线y=x交于点D.试判断DF+EF与2BC的大小,并说明理由.
的图象上,过B、E两点作x轴的垂线,垂足分别为C、F,直线EF与直线y=x交于点D.试判断DF+EF与2BC的大小,并说明理由.
解:DF+EF>2BC.理由如下:
联立 ,解得
,解得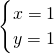 或
或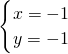 ,
,
∴点B的坐标为(1,1),
∴BC=1;
设D的坐标为(a,a),a≠1,
∵EF⊥x轴,
∴E点的横坐标为a,
把x=a代入y= =
= ,
,
∴E点坐标为(a, ),
),
∴DF=|a|,EF=| |,
|,
∴|a|+| |=(|a|-|
|=(|a|-| |)2+2>2,
|)2+2>2,
∵a≠1,
∴(|a|-| |)2>0,
|)2>0,
∴|a|+| |>2,
|>2,
∴DF+EF>2BC.
分析:先解方程组 得到B点坐标(1,1),则BC=1;然后设D的坐标为(a,a),a≠1,则E点的横坐标为a,利用E在函数y=
得到B点坐标(1,1),则BC=1;然后设D的坐标为(a,a),a≠1,则E点的横坐标为a,利用E在函数y= 图象上得到E点坐标为(a,
图象上得到E点坐标为(a, ),得到DF=|a|,EF=|
),得到DF=|a|,EF=| |,根据|a|+|
|,根据|a|+| |=(|a|-|
|=(|a|-| |)2+2>2,即可得到DF+EF>2BC.
|)2+2>2,即可得到DF+EF>2BC.
点评:本题考查了反比例函数综合题:点在图象上,则点的横纵坐标满足图象的解析式;两图象的交点坐标就是由两个图象的解析式所组成的方程组的解.也考查了一次函数以及代数式的变形能力.
联立
 ,解得
,解得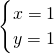 或
或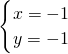 ,
,∴点B的坐标为(1,1),
∴BC=1;
设D的坐标为(a,a),a≠1,
∵EF⊥x轴,
∴E点的横坐标为a,
把x=a代入y=
 =
= ,
,∴E点坐标为(a,
 ),
),∴DF=|a|,EF=|
 |,
|,∴|a|+|
 |=(|a|-|
|=(|a|-| |)2+2>2,
|)2+2>2,∵a≠1,
∴(|a|-|
 |)2>0,
|)2>0,∴|a|+|
 |>2,
|>2,∴DF+EF>2BC.
分析:先解方程组
 得到B点坐标(1,1),则BC=1;然后设D的坐标为(a,a),a≠1,则E点的横坐标为a,利用E在函数y=
得到B点坐标(1,1),则BC=1;然后设D的坐标为(a,a),a≠1,则E点的横坐标为a,利用E在函数y= 图象上得到E点坐标为(a,
图象上得到E点坐标为(a, ),得到DF=|a|,EF=|
),得到DF=|a|,EF=| |,根据|a|+|
|,根据|a|+| |=(|a|-|
|=(|a|-| |)2+2>2,即可得到DF+EF>2BC.
|)2+2>2,即可得到DF+EF>2BC.点评:本题考查了反比例函数综合题:点在图象上,则点的横纵坐标满足图象的解析式;两图象的交点坐标就是由两个图象的解析式所组成的方程组的解.也考查了一次函数以及代数式的变形能力.

练习册系列答案
相关题目
 如图,点A是函数y=
如图,点A是函数y= 如图,点B是函数
如图,点B是函数 如图,点M是函数
如图,点M是函数
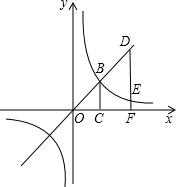 如图,点B是函数y=
如图,点B是函数y=