题目内容
 如图,点A是函数y=
如图,点A是函数y=| 1 |
| x |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| x |
| 2 |
| 1 |
| x |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
分析:本题给出了角平分线,给出了两条线段的定值差,因此可通过构建等腰三角形作出这个等值差进行求解.
解答: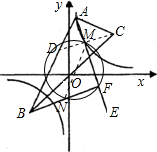 解:如图:过C作CD⊥AF,垂足为M,交AB于D,
解:如图:过C作CD⊥AF,垂足为M,交AB于D,
∵AF平分∠BAC,且AM是DC边上的高,
∴△DAC是等腰三角形,
∴AD=AC,
∴BD=AB-AC=2
,
即BD长为定值,
过M作MN∥BD于N,
则四边形MNBD是个平行四边形,
∴MN=BD,
在△MNF中,无论F怎么变化,有两个条件不变:
①MN的长为定值,②∠MFN=90°,
因此如果作△MNF的外接圆,那么F点总在以MN为直径的圆上运动,因此F点的运动轨迹应该是个圆.
∴圆的直径为MN,且MN=BD,BD=AB-AC=2
,
∴圆的半径为
.
故选C.
 解:如图:过C作CD⊥AF,垂足为M,交AB于D,
解:如图:过C作CD⊥AF,垂足为M,交AB于D,∵AF平分∠BAC,且AM是DC边上的高,
∴△DAC是等腰三角形,
∴AD=AC,
∴BD=AB-AC=2
| 2 |
即BD长为定值,
过M作MN∥BD于N,
则四边形MNBD是个平行四边形,
∴MN=BD,
在△MNF中,无论F怎么变化,有两个条件不变:
①MN的长为定值,②∠MFN=90°,
因此如果作△MNF的外接圆,那么F点总在以MN为直径的圆上运动,因此F点的运动轨迹应该是个圆.
∴圆的直径为MN,且MN=BD,BD=AB-AC=2
| 2 |
∴圆的半径为
| 2 |
故选C.
点评:本题以反比例函数为背景,结合了等腰三角形的知识、平行四边形的知识、直角三角形的知识、三角形外接圆的知识等.综合性强.在本题中能够找出AB、AC的等值差以及让F与这个等值差相关联是解题的关键.

练习册系列答案
相关题目
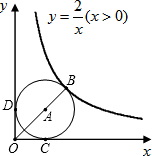 如图,点B是函数
如图,点B是函数 如图,点M是函数
如图,点M是函数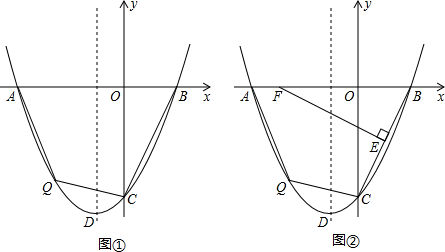
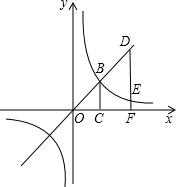 如图,点B是函数y=
如图,点B是函数y=